Computationally, this is a harder problem. Mathematically, we can typically solve problems when we have a number of equations equal to or greater than the number of unknowns. For data points ind dimensions and clusters, we have equations and unknowns. This means we have a harder problem to solve.
Clustering is a stochastic (random) algorithm, so it can be a little harder to debug the models and measure performance. For this reason, we are going to look a little more closely at what it actually does than we did with classification.
import matplotlib.pyplot as plt
import numpy as np
import itertools
import seaborn as sns
import pandas as pd
from sklearn import datasets
from sklearn.cluster import KMeans
from sklearn import metrics
import string
import itertools as it
import imageio.v3 as iio # for making gifs to save
# set global random seed so that the notes are the same each time the site builds
rand_seed =398
np.random.seed(rand_seed)How does Kmeans work?¶
We will start with some synthetic data and then see how the clustering works. This data is set so that the algorithm works well for sure and is unlikely to get stuck.
This code should be fairly readable, but is not strictly required.
One tricky part is zip which is a builtin fuction for iteratinv over groups of things together.
And itertools is a core library for related more iterating.
One way to understand this block of code is to try changing the parameters (the top section) and see how they effect the plots. The var and spacing will have the most impact on the clustering performance.
# ------ Set paramters, change these to adjust the sample
# number of classes (groups)
C = 4
# number of dimensions of the features
D=2
# number of samples
N = 200
# minimum of the means
offset = 2
# distance between means
spacing = 2
# set the variance of the blobs
var = .25
# ------ Get the class labels
# choose the first C uppcase letters using the builtin string class
classes = list(string.ascii_uppercase[:C])
# ----- Pick some means
# get the number of grid locations needed
G = int(np.ceil(np.sqrt(C)))
# get the locations for each axis
grid_locs = a = np.linspace(offset,offset+G*spacing,G)
# compute grid (i,j) for each combination of values above & keep C values
means = [(i,j) for i, j in it.product(grid_locs,grid_locs)][:C]
# store in dictionary with class labels
mu = {c: i for c, i in zip(classes,means)}
# ----- Sample the data
#randomly choose a class for each point, with equal probability
clusters_true = np.random.choice(classes,N)
# draw a random point according to the means from above for each point
data = [np.random.multivariate_normal(mu[c], var*np.eye(D)) for c in clusters_true]
# ----- Store in a dataframe
# rounding to make display neater later
df = pd.DataFrame(data = data,columns = ['x' + str(i) for i in range(D)]).round(2)
# add true cluster
df['true_cluster'] = clusters_trueThis gives us a small dataframe with 2 features and 4 clusters[1].
df.head()We can see the data two different ways:
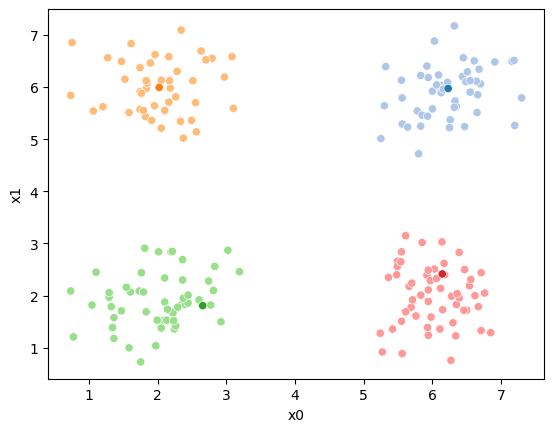
sns.scatterplot(data =df,x='x0',y='x1',hue='true_cluster')<Axes: xlabel='x0', ylabel='x1'>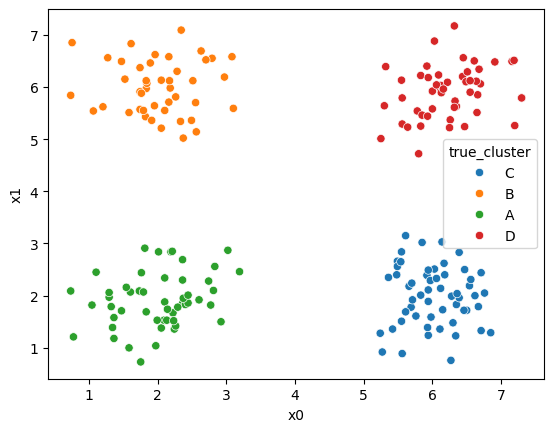
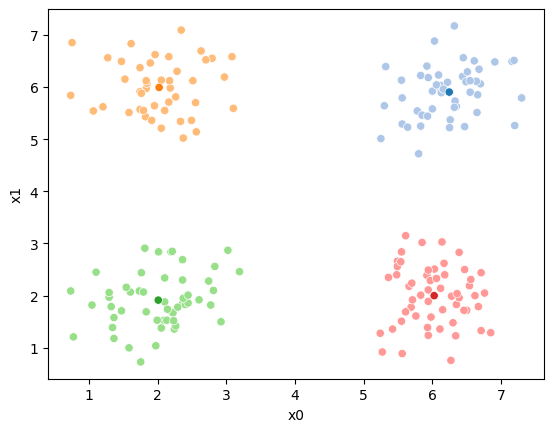
sns.scatterplot(data =df,x='x0',y='x1',color='lightgray',legend=False)<Axes: xlabel='x0', ylabel='x1'>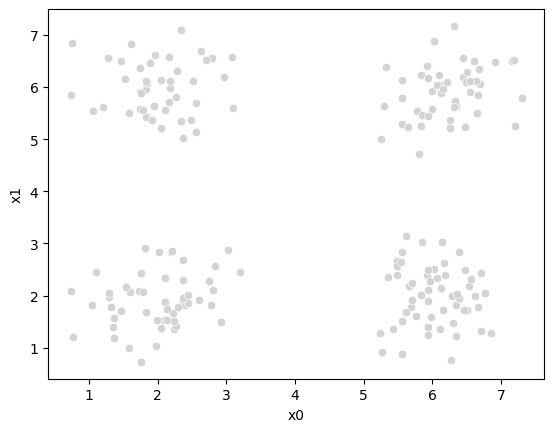
It’s all the same points, but Kmeans does not get the true_cluster column. We used that to generate the data, but it is not used by the KMeans algorithm.
Setup¶
First we will make a variable that we can use to pick out the feature columns
data_cols = ['x0','x1']Next, we’ll set up some helper code.
For more on color palettes see the seaborn docs
def mu_to_df(mu,i):
'''
take a numpy array and make a small df with columns for the features, class label and a type column so it can be combined with other data later
'''
mu_df = pd.DataFrame(mu,columns=['x0','x1'])
mu_df['iteration'] = str(i)
mu_df['class'] = ['M'+str(i) for i in range(K)]
mu_df['type'] = 'mu'
return mu_dfWe want to make plots with the data and the means visible. I would like to have the points in pale colors and the means in bold.
You can see that the seaborn tab20 pallete is paired colors:
sns.color_palette('tab20',8)The cmap_pt and cmap_mu takes the odd and even subsets of the palette into two separate palettes.
cmap_pt = sns.color_palette('tab20',8)[1::2]
cmap_mu = sns.color_palette('tab20',8)[0::2]Remember the third number in an iterator is the step, so we can take every nth element from an iterable like: [0, 2, 4, 6, 8] or [1, 3, 5, 7, 9]
Initializing the algorithm¶
Kmeans starts by setting K, we will use 4 to match the correct valued for our data.
K =CWe could set this differently, but our firs time through we want to see it work well
Exercise 1 (Explore this algorithm)
Try changing this number manually and seeing how things change to understand better.
You can download this file as a myst notebook from the download icon at the top of the page and if you have jupytext you can right click on the file then select “Notebook” from “Open with”
This is an iterative algorithm, so we will initialize a counter variable so we can track how many times it goes through its steps.
i =0The last part of the initialization is to select 4 points to be our initial means[1]:
mu0 = df[data_cols].sample(n=K).values
mu0array([[5.56, 5.79],
[5.3 , 5.64],
[2.26, 1.42],
[6.35, 5.63]])Now, we will use our helper function to make them easier to read and label them for later use:
mu_df = mu_to_df(mu0,i)
mu_dfAnd visualize, by updating our plot:
sfig = sns.scatterplot(data =df,x='x0',y='x1',color='lightgray',legend=False)
# plt.plot(mu[:,0],mu[:,1],marker='s',linewidth=0)
mu_df = mu_to_df(mu0,i)
sns.scatterplot(data =mu_df,x='x0',y='x1',hue='class',palette=cmap_mu,ax=sfig,legend=False)<Axes: xlabel='x0', ylabel='x1'>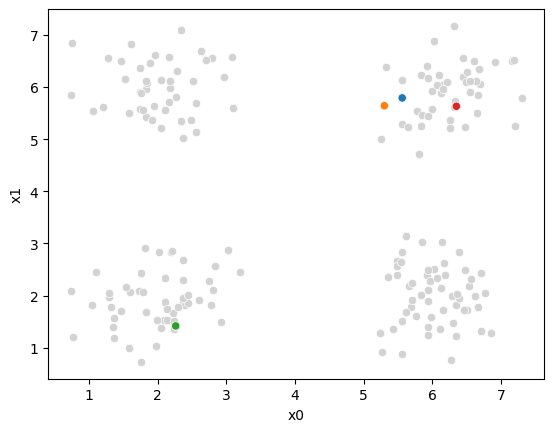
At this piont, we have all the points, but no labels for them, and we have these 4 points as our means.
Assignment step¶
Now, we will compute, for each sample, which of those 4 points it is closest to first by taking the difference, squaring it, then summing along each row.
To compute the distance we will first subtract from the mean:
(df[data_cols].loc[0]- mu0[0])x0 0.27
x1 -3.78
Name: 0, dtype: float64then square each
((df[data_cols].loc[0]- mu0[0])**2)x0 0.0729
x1 14.2884
Name: 0, dtype: float64and sum
((df[data_cols].loc[0]- mu0[0])**2).sum()np.float64(14.361300000000002)If we needed the right units on these distances, we would also sqrt but, we actually will just use the distances to figure out which mean is closes to the each point. If then so we do not need the sqrt to get the right end answer so we can save that step, which saves computation.
we can do this fo all of the rows
((df[data_cols]- mu0[0])**2).sum(axis=1)0 14.3613
1 20.3125
2 19.9274
3 9.0682
4 15.9188
...
195 32.1458
196 8.7125
197 21.2141
198 0.3200
199 31.0472
Length: 200, dtype: float64then we can do this for all four means:
[((df[data_cols]- mu_i)**2).sum(axis=1) for mu_i in mu0][0 14.3613
1 20.3125
2 19.9274
3 9.0682
4 15.9188
...
195 32.1458
196 8.7125
197 21.2141
198 0.3200
199 31.0472
Length: 200, dtype: float64,
0 13.4578
1 17.9876
2 18.9745
3 7.5661
4 13.8553
...
195 28.8965
196 7.5344
197 20.5642
198 0.2837
199 27.8161
Length: 200, dtype: float64,
0 13.0930
1 18.4144
2 14.8261
3 18.4025
4 17.1905
...
195 1.3505
196 26.2036
197 19.8106
198 25.9405
199 2.4065
Length: 200, dtype: float64,
0 13.3748
1 27.9922
2 18.2905
3 14.4449
4 22.7673
...
195 38.3485
196 14.1146
197 18.6196
198 0.6641
199 37.6749
Length: 200, dtype: float64]This gives us a list of 4 data DataFrames, one for each mean (array([[5.56, 5.79],
[5.3 , 5.64],
[2.26, 1.42],
[6.35, 5.63]])), with one row
for each point in the dataset with the distance from that point to the
corresponding mean. We can concatenate these horizontally (axis=1) these into one DataFrame.
If you could not run this part in class, jump down to the solution and then come back
pd.concat([((df[data_cols]- mu_i)**2).sum(axis=1) for mu_i in mu0],axis=1).head()Now we have one row per sample and one column per mean, with with the distance from that point to the mean. What we want is to calculate the assignment, which
mean is closest, for each point. Using idxmin with axis=1 we take the
minimum across each row and returns the index (location) of that minimum.
pd.concat([((df[data_cols]- mu_i)**2).sum(axis=1) for mu_i in mu0],axis=1).idxmin(axis=1)0 2
1 1
2 2
3 1
4 1
..
195 2
196 1
197 3
198 1
199 2
Length: 200, dtype: int64We’ll save all of this in a column named '0'. Since it is our 0th iteration.
This is called the assignment step.
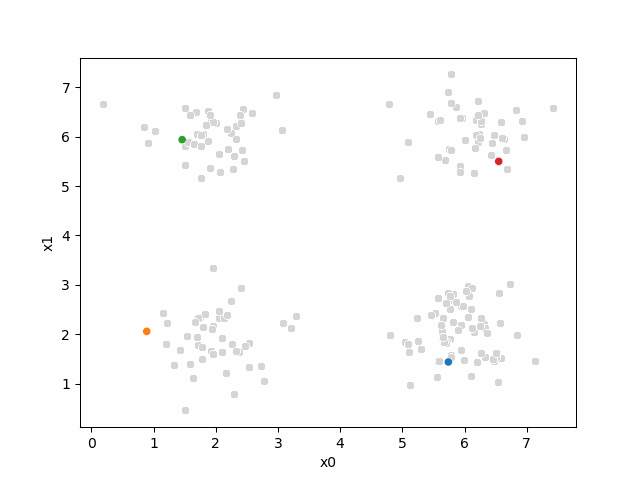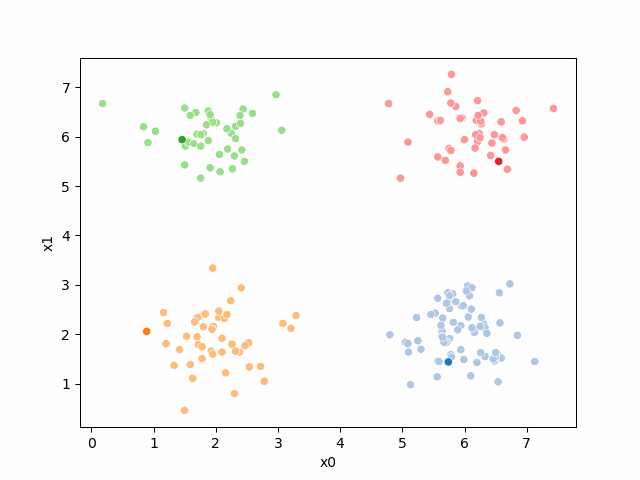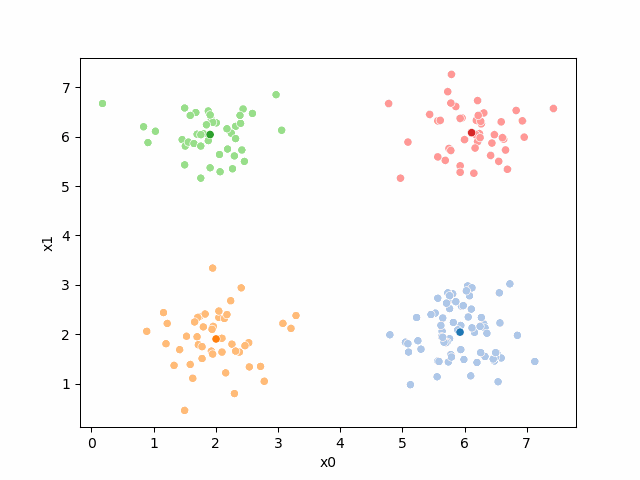
df[str(i)] = pd.concat([((df[data_cols]- mu_i)**2).sum(axis=1) for mu_i in mu0],axis=1).idxmin(axis=1)to see what we have:
df.head()andd now we can re-plot, we still have the same means, but now we use the '0' column to give the points each a color.
Now we can plot the data, save the axis, and plot the means on top of that.
Seaborn plotting functions return an axis, by saving that to a variable, we
can pass it to the ax parameter of another plotting function so that both
plotting functions go on the same figure.
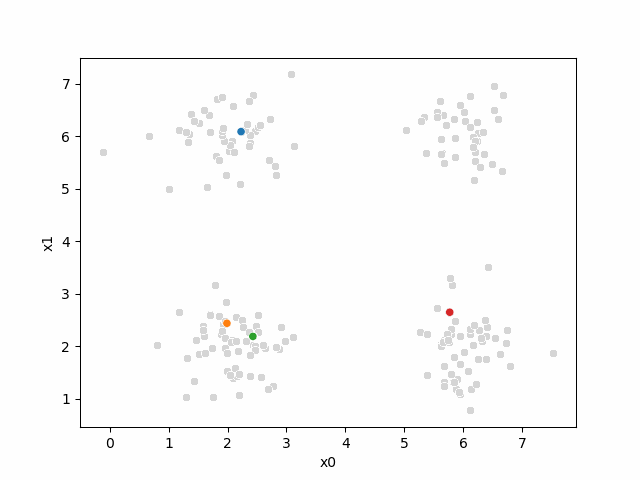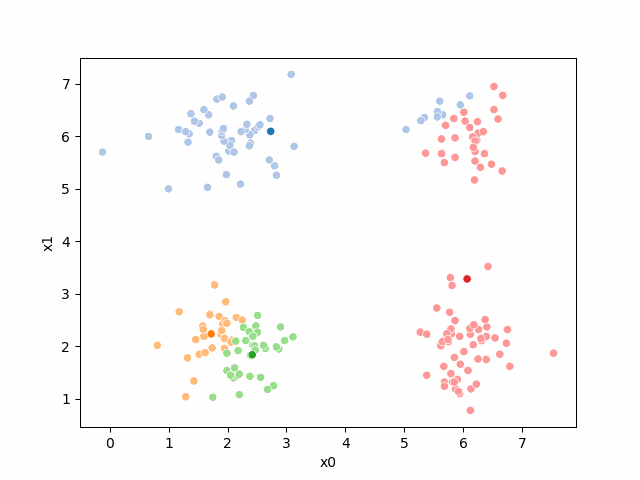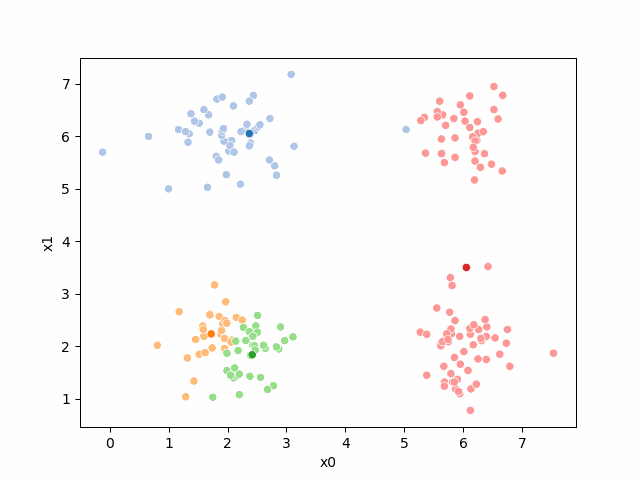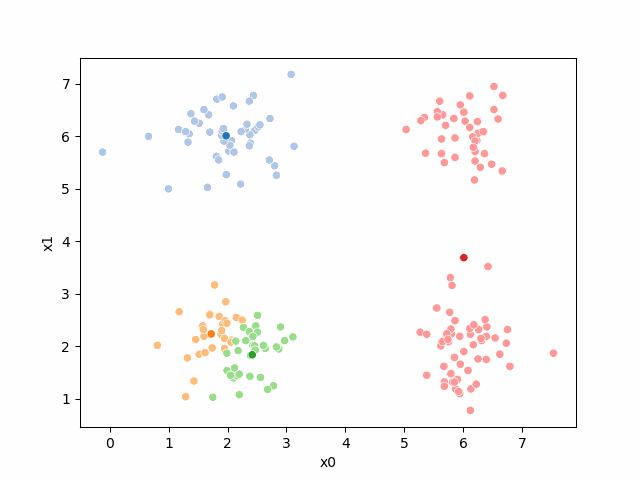
sfig = sns.scatterplot(data =df,x='x0',y='x1',hue='0',palette=cmap_pt,legend=False)
# plt.plot(mu[:,0],mu[:,1],marker='s',linewidth=0)
mu_df = mu_to_df(mu0,i)
sns.scatterplot(data =mu_df,x='x0',y='x1',hue='class',palette=cmap_mu,
ax=sfig,legend=False)<Axes: xlabel='x0', ylabel='x1'>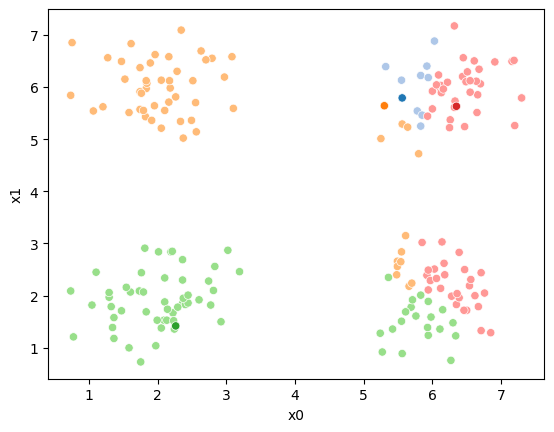
this strategy of saving the plot axes to add an additional plot is a common way to make more complicated plots, something you might use in your extensions
We see that each point is assigned to the lighter shade of its matching mean. These points are the one that is closest to each point, but they’re not the centers of the point clouds. Now, we can compute new means of the points assigned to each cluster, using groupby.
Updating the means¶
mu1 = df.groupby('0')[data_cols].mean().valuesWe can plot these again, the same data, but with the new means.
fig = plt.figure()
mu_df = mu_to_df(mu1,1)
sfig = sns.scatterplot(data =df,x='x0',y='x1',hue='0',palette=cmap_pt,legend=False)
sns.scatterplot(data =mu_df,x='x0',y='x1',hue='class',palette=cmap_mu,ax=sfig,legend=False)
sfig.get_figure().savefig('kmeans02.png')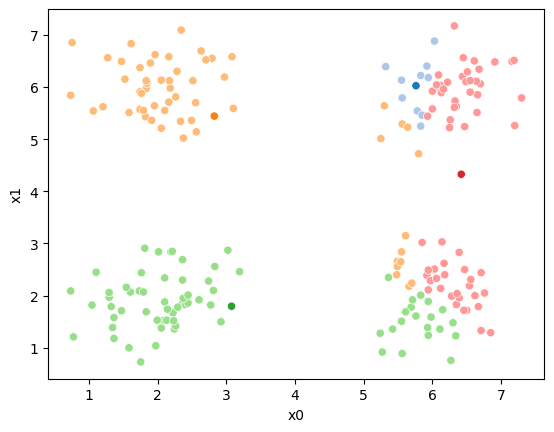
We see that now the means are in the center of each cluster, but that there are now points in one color that are assigned to other clusters.
So, again we can update the assignments.
i=1 #increment
df[str(i)] = pd.concat([((df[data_cols]-mu_i)**2).sum(axis=1) for mu_i in mu1],axis=1).idxmin(axis=1)
df.head()And plot again:
sfig = sns.scatterplot(data =df,x='x0',y='x1',hue=str(i),palette=cmap_pt,legend=False)
# plt.plot(mu[:,0],mu[:,1],marker='s',linewidth=0)
mu_df = mu_to_df(mu1,i)
sns.scatterplot(data =mu_df,x='x0',y='x1',hue='class',palette=cmap_mu,ax=sfig,legend=False)
sfig.get_figure().savefig('kmeans03.png')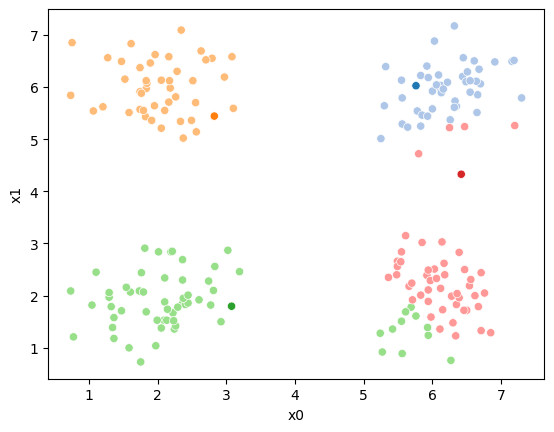
we see it improves by the means moved to the center of each color.
Iterating to completion¶
If we keep going back and forth like this, eventually, the assignment step will not change any assignments. We call this condition convergence. We can implement the algorithm with a while loop.
We will set the stopping criterion to be 0 changed assignments.
mu_list = [mu_to_df(mu0,0),mu_to_df(mu1,1)]
cur_old = str(i-1)
cur_new = str(i)
curmu = mu1
number_changed_assignments = sum(df[cur_old] !=df[cur_new])
while number_changed_assignments >0:
cur_old = cur_new
i +=1
cur_new = str(i)
# update the means and plot with current generating assignments
curmu = df.groupby(cur_old)[data_cols].mean().values
mu_df = mu_to_df(curmu,i)
mu_list.append(mu_df)
fig = plt.figure()
# plot with old assignments
sfig = sns.scatterplot(data =df,x='x0',y='x1',hue=cur_old,palette=cmap_pt,legend=False)
sns.scatterplot(data =mu_df,x='x0',y='x1',hue='class',palette=cmap_mu,ax=sfig,legend=False)
# save image to combine into a gif for the notes (do not need to do this)
file_num = str(i*2 ).zfill(2)
sfig.get_figure().savefig('kmeans' +file_num + '.png')
# update the assigments and plot with the associated means
df[cur_new] = pd.concat([((df[data_cols]-mu_i)**2).sum(axis=1) for mu_i in curmu],axis=1).idxmin(axis=1)
fig = plt.figure()
sfig = sns.scatterplot(data =df,x='x0',y='x1',hue=cur_new,palette=cmap_pt,legend=False)
sns.scatterplot(data =mu_df,x='x0',y='x1',hue='class',palette=cmap_mu,ax=sfig,legend=False)
# save image to combine into a gif for the notes (do not need to do this)
# we are making 2 images per iteration
file_num = str(i*2+1).zfill(2)
sfig.get_figure().savefig('kmeans' +file_num + '.png')
number_changed_assignments = sum(df[cur_old] !=df[cur_new])
print( 'iteration ' + str(i))iteration 2
iteration 3
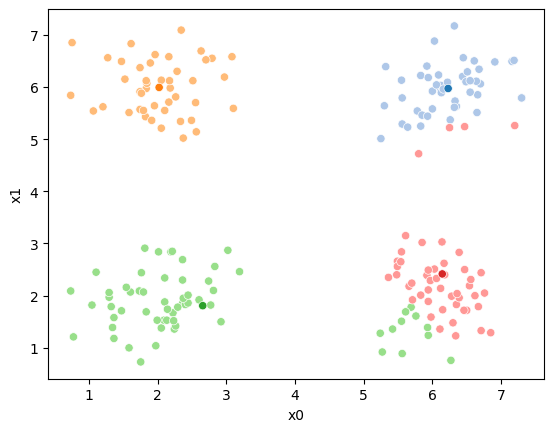

animated¶
Notebook Cell
# make a gif to load
# write the file names
img_files = ['kmeans' + str(ii).zfill(2) +'.png' for ii in range(i*2+1)]
# load the imges back
images = np.stack([iio.imread(img_file) for img_file in img_files],axis=0)
# write as gif
iio.imwrite('kmeans'+str(rand_seed) + '.gif', images,loop=0,duration=1000,plugin='pillow') # Adjust duration as needed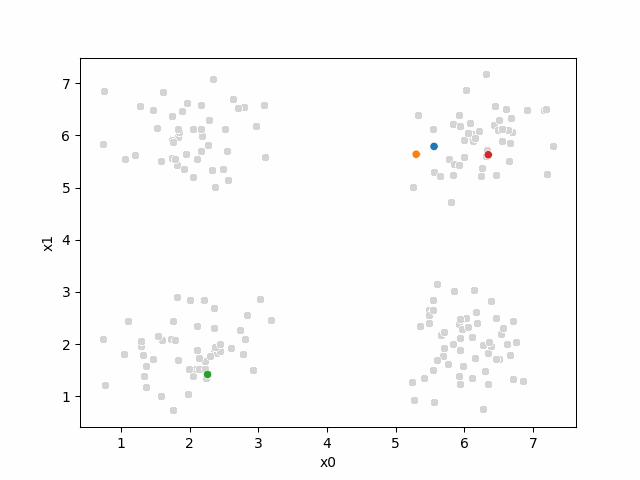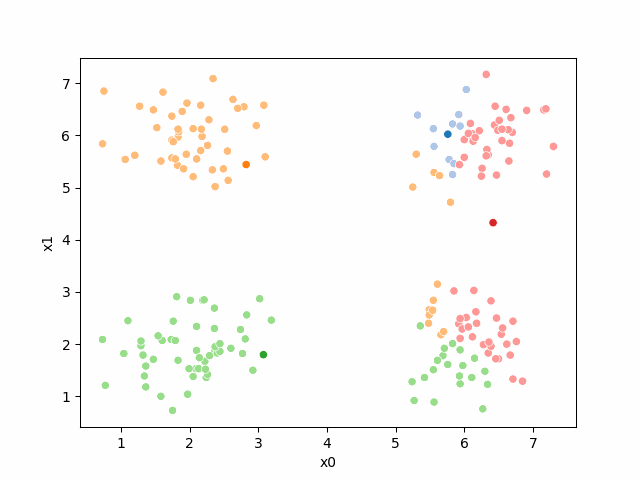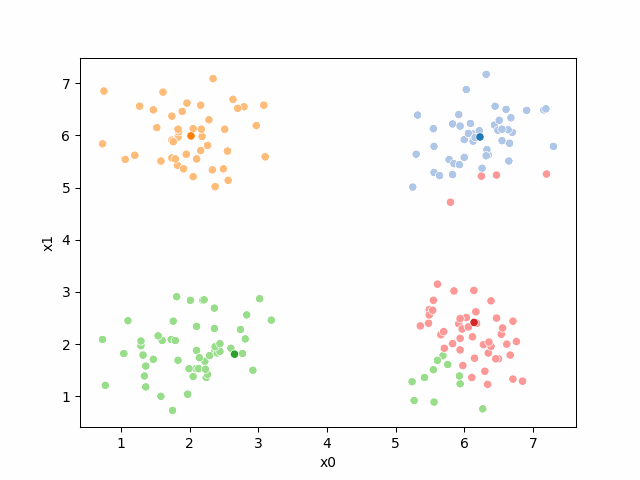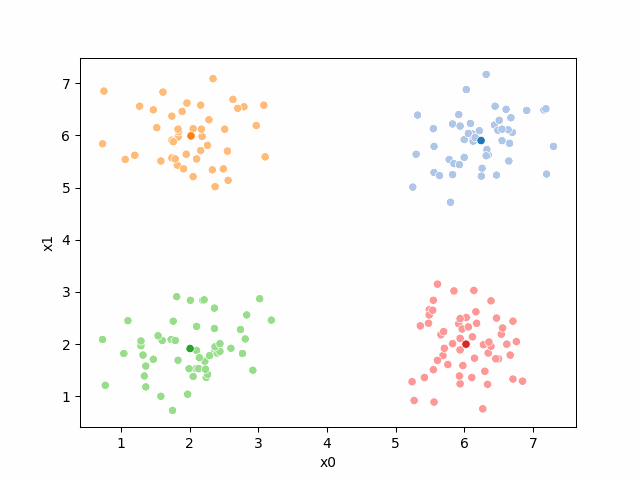
Here are some other runs that I saved. I updated this notebook so that it saved the final gif as a different name based on the random seed, ran it a few times with different seeds then kept one I thought was a good visualization above.
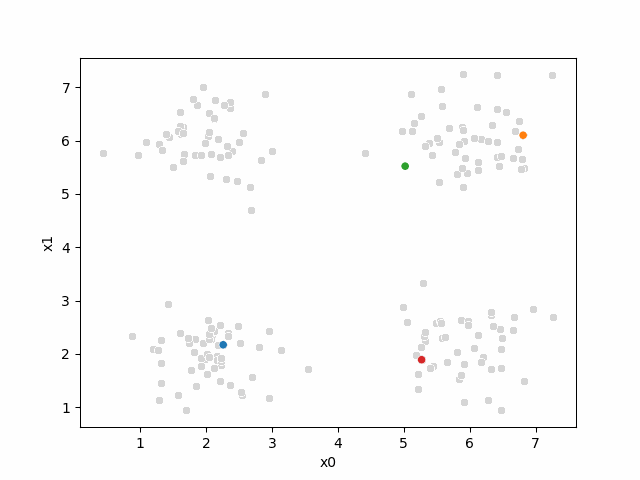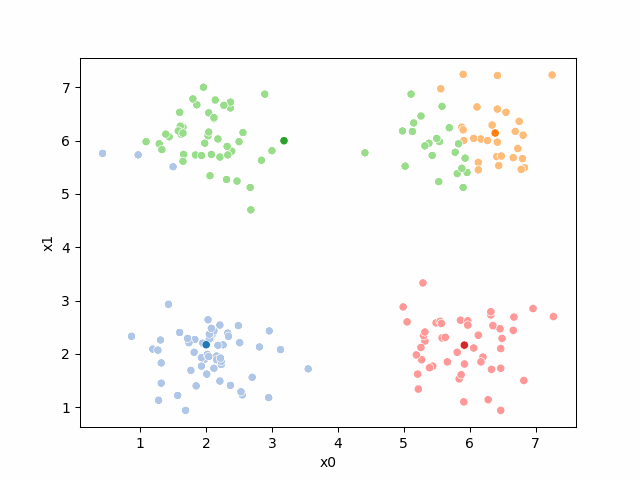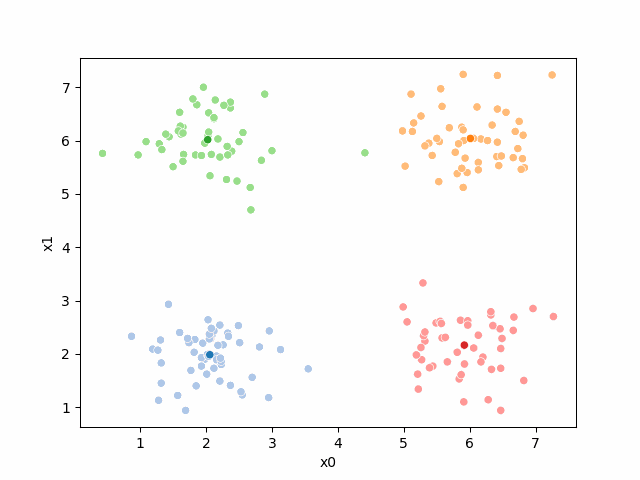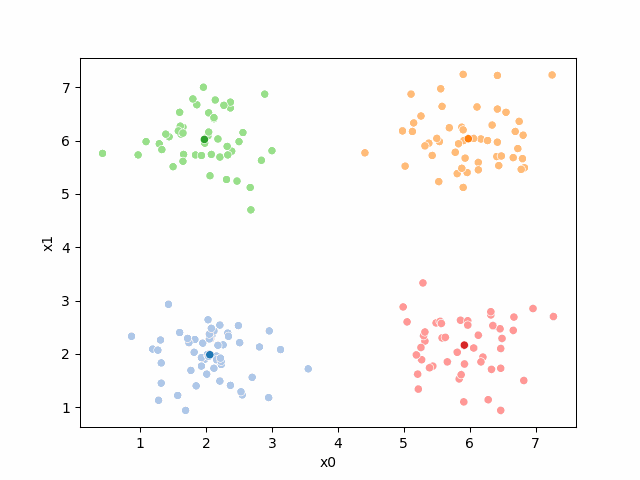
Including this on were it got stuck:
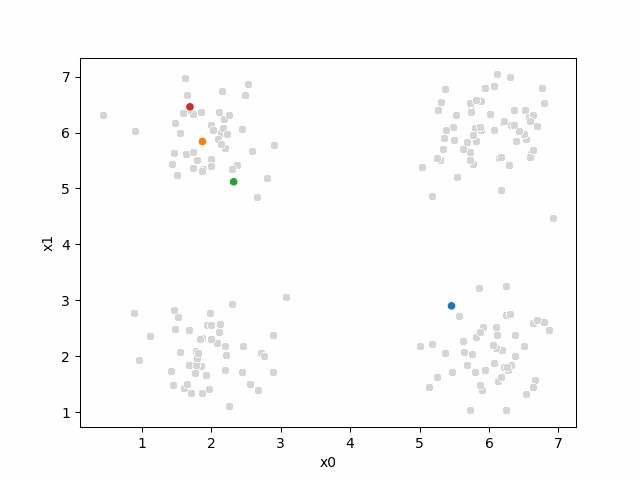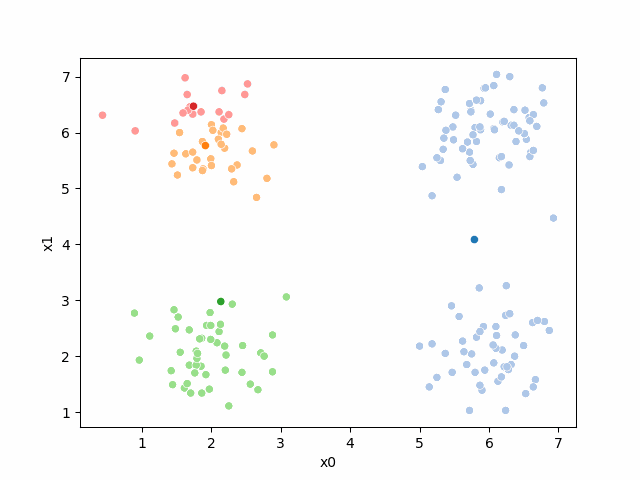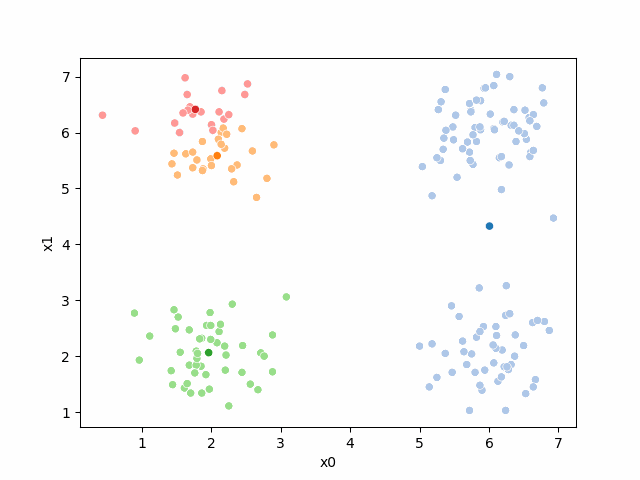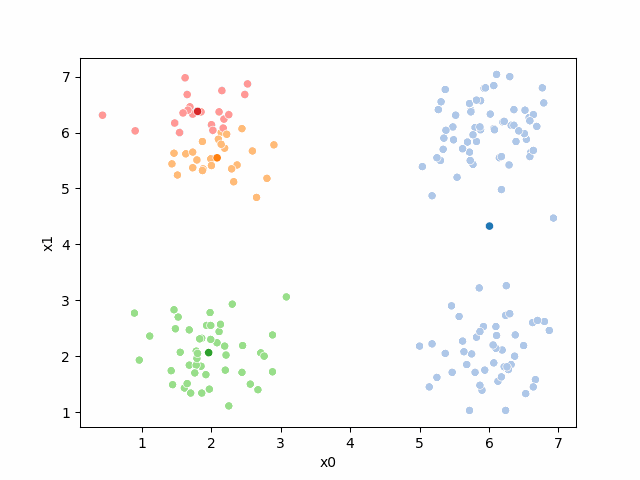
storyboard¶
We can also make them a grid:
df_vis = df.melt(id_vars = ['x0','x1'], var_name ='iteration',value_name='class')
df_vis.replace({'class':{i:c for i,c in enumerate(string.ascii_uppercase[:C])}},inplace=True)
df_vis['type'] = 'pt'
df_mu_vis = pd.concat([pd.concat(mu_list),df_vis])
cmap = sns.color_palette('tab20',8)
n_iter = i
sfig = sns.relplot(data=df_mu_vis,x='x0',y='x1',hue='class',col='iteration',
col_wrap=3,hue_order = ['M0','A','M1','B','M2','C','M3','D'],
palette = cmap,size='type',col_order=[str(i) for i in range(n_iter+1)])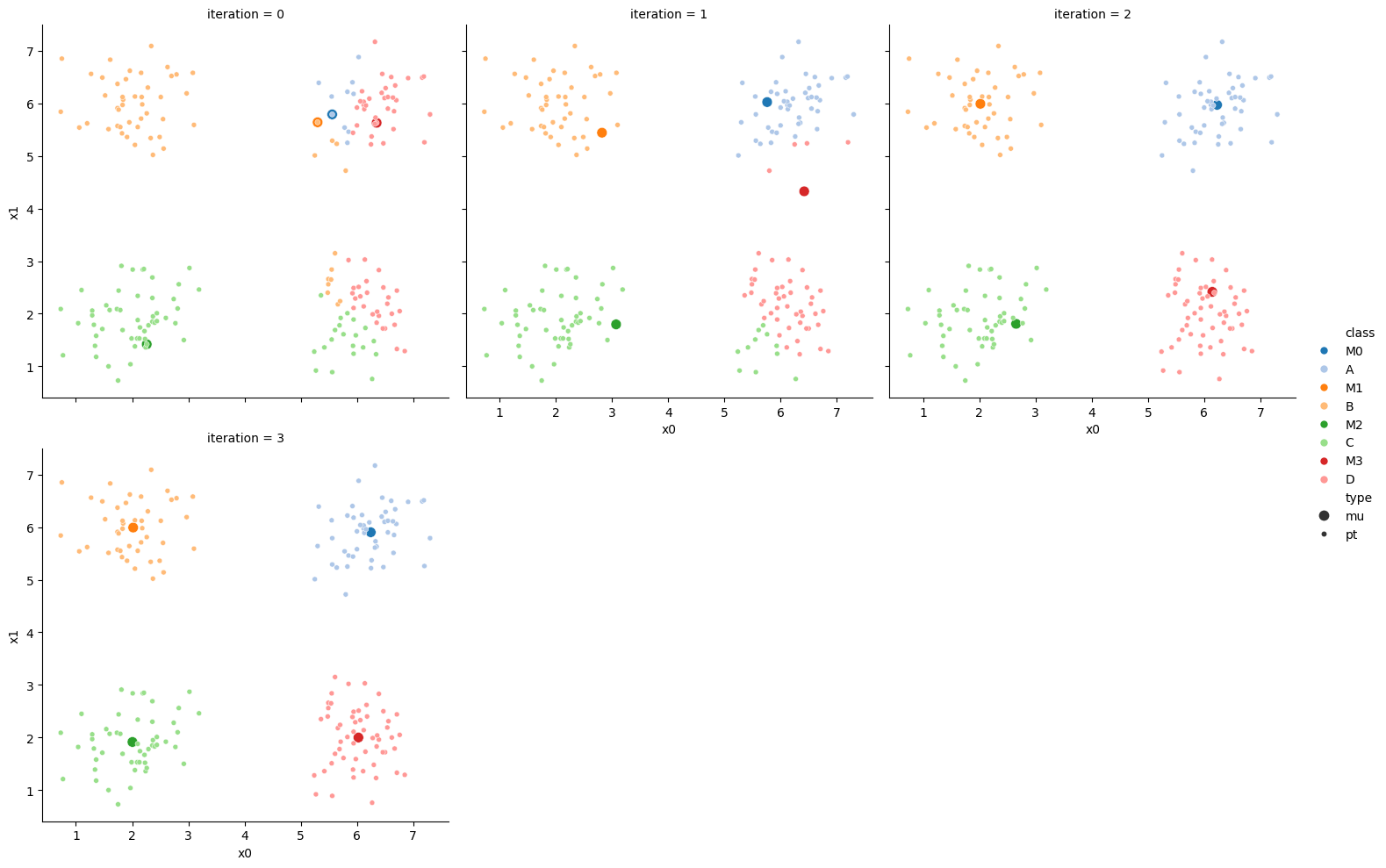
More metrics¶
We’ll go back to the iris data
iris_df =sns.load_dataset('iris')
sns.pairplot(iris_df)<seaborn.axisgrid.PairGrid at 0x7fb9b70bb2c0>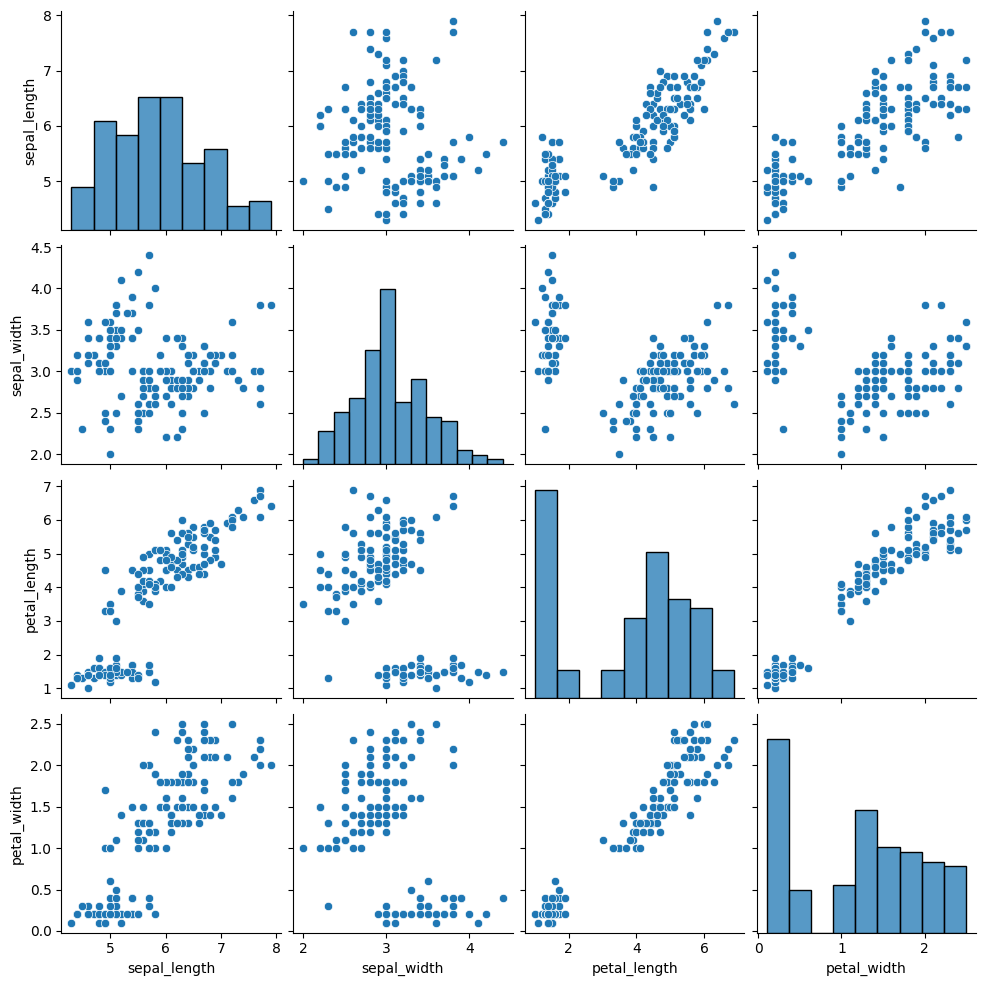
first let’s cluster it again:
measurement_cols = ['sepal_length','petal_length','sepal_width','petal_width']
iris_X = iris_df[measurement_cols]we’ll create our object
km3 = KMeans(n_clusters=3)and save the predictions
y_pred = km3.fit_predict(iris_X)
y_pred[:5]array([1, 1, 1, 1, 1], dtype=int32)In class, we ran the algorithm a few times and saw that the number changed
We saw the silhouette score last class, which is a true clustering method, so we can use that to see if a clustring algorithm has succeeded on in a real use case where we actually do not have the labels. However if we were checkinng if our implementation of a clustering algorithm worked or if our new clustering algorithm worked, we would test with the actual labels that we do have to know if the algorithm found the same groups we had. We might also want to in a real clustering context see if two different runs of a clustering algorithm were the same, or if two different algorithms on the same data found the same solution. In this case we can use other metrics, like mutual information.
Mutual information measures how much knowing one variable tells about another. It can be interpretted like a correlation for categorical variables.
metrics.adjusted_mutual_info_score(iris_df['species'],y_pred)0.7386548254402864This score is pretty good, but not perfect, but the classification with the labels was not either so that makes sense
A variable has 1 AMI with itself:
metrics.adjusted_mutual_info_score(iris_df['species'],iris_df['species'])1.0and uncorrelated thing have AMI near 0
metrics.adjusted_mutual_info_score(np.random.choice(4,size=100),
np.random.choice(4,size=100))-0.010969097229447335Ufunc error¶
A few of you had an error in class. I was able to replicate it! (and thanks to the student who emailed about what they learned)
[df[data_cols] - mui for mui in mu]---------------------------------------------------------------------------
UFuncTypeError Traceback (most recent call last)
Cell In[41], line 1
----> 1 [df[data_cols] - mui for mui in mu]
File ~/.local/lib/python3.12/site-packages/pandas/core/ops/common.py:76, in _unpack_zerodim_and_defer.<locals>.new_method(self, other)
72 return NotImplemented
74 other = item_from_zerodim(other)
---> 76 return method(self, other)
File ~/.local/lib/python3.12/site-packages/pandas/core/arraylike.py:194, in OpsMixin.__sub__(self, other)
192 @unpack_zerodim_and_defer("__sub__")
193 def __sub__(self, other):
--> 194 return self._arith_method(other, operator.sub)
File ~/.local/lib/python3.12/site-packages/pandas/core/frame.py:7935, in DataFrame._arith_method(self, other, op)
7932 self, other = self._align_for_op(other, axis, flex=True, level=None)
7934 with np.errstate(all="ignore"):
-> 7935 new_data = self._dispatch_frame_op(other, op, axis=axis)
7936 return self._construct_result(new_data)
File ~/.local/lib/python3.12/site-packages/pandas/core/frame.py:7967, in DataFrame._dispatch_frame_op(self, right, func, axis)
7964 right = lib.item_from_zerodim(right)
7965 if not is_list_like(right):
7966 # i.e. scalar, faster than checking np.ndim(right) == 0
-> 7967 bm = self._mgr.apply(array_op, right=right)
7968 return self._constructor_from_mgr(bm, axes=bm.axes)
7970 elif isinstance(right, DataFrame):
File ~/.local/lib/python3.12/site-packages/pandas/core/internals/managers.py:361, in BaseBlockManager.apply(self, f, align_keys, **kwargs)
358 kwargs[k] = obj[b.mgr_locs.indexer]
360 if callable(f):
--> 361 applied = b.apply(f, **kwargs)
362 else:
363 applied = getattr(b, f)(**kwargs)
File ~/.local/lib/python3.12/site-packages/pandas/core/internals/blocks.py:395, in Block.apply(self, func, **kwargs)
389 @final
390 def apply(self, func, **kwargs) -> list[Block]:
391 """
392 apply the function to my values; return a block if we are not
393 one
394 """
--> 395 result = func(self.values, **kwargs)
397 result = maybe_coerce_values(result)
398 return self._split_op_result(result)
File ~/.local/lib/python3.12/site-packages/pandas/core/ops/array_ops.py:283, in arithmetic_op(left, right, op)
279 _bool_arith_check(op, left, right) # type: ignore[arg-type]
281 # error: Argument 1 to "_na_arithmetic_op" has incompatible type
282 # "Union[ExtensionArray, ndarray[Any, Any]]"; expected "ndarray[Any, Any]"
--> 283 res_values = _na_arithmetic_op(left, right, op) # type: ignore[arg-type]
285 return res_values
File ~/.local/lib/python3.12/site-packages/pandas/core/ops/array_ops.py:218, in _na_arithmetic_op(left, right, op, is_cmp)
215 func = partial(expressions.evaluate, op)
217 try:
--> 218 result = func(left, right)
219 except TypeError:
220 if not is_cmp and (
221 left.dtype == object or getattr(right, "dtype", None) == object
222 ):
(...) 225 # Don't do this for comparisons, as that will handle complex numbers
226 # incorrectly, see GH#32047
UFuncTypeError: ufunc 'subtract' did not contain a loop with signature matching types (dtype('float64'), dtype('<U1')) -> NoneThis is because I changed from overwriting the variable mu which is a dict to using using new variables, mu0 and mu1 which are numpy.ndarray
recall the initial mu is the set up for generating data:
mu{'A': (np.float64(2.0), np.float64(2.0)),
'B': (np.float64(2.0), np.float64(6.0)),
'C': (np.float64(6.0), np.float64(2.0)),
'D': (np.float64(6.0), np.float64(6.0))}if iterate over a dict then we get the keys (here the class labels) instead of the values (here the true means)
[mui for mui in mu]['A', 'B', 'C', 'D']We cannot subtract characters from floats, so it gave an error.
At least one person used AI for an answer, which makes the code run, but is wrong, conceptually.
The correct solution is to use mu0 instead of mu. If you use mu.values, then you subtract the true means used to generate the data instead of the ones that had been computed.
It is a UfuncTypeError because in numpy the universal functions (ufunc) are used for functions that operate element wise on numpy arrays (which is what we were doing with the subtraction).
This tells us that the way python parses the subtraction in this case is to extract the values from the pd.DataFrame to get two np.ndarray and use the numpy subtract function.
Even operators like -, +, < etc are implemented as methods of object classes, so if in Python, you are creating your own objects you can add a special method to the objec to be able to use operators with your objects
You can install all libraries with:
conda env update --name rhodyds --file https://raw.githubusercontent.com/rhodyprog4ds/BrownFall25/refs/heads/main/rhodyds_environment.ymlQuestions¶
How can I request a regrade¶
See syllabus
Can deploying a model earn innovate?¶
Maybe, make an issue with more detail about your idea.