20. Learning Curves and more Model Comparison#
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import pandas as pd
from sklearn import datasets
from sklearn import cluster
from sklearn import svm
from sklearn import tree
# import the whole model selection module
from sklearn import model_selection
sns.set_theme(palette='colorblind')
# load and split the data
iris_X, iris_y = datasets.load_iris(return_X_y=True)
iris_X_train, iris_X_test, iris_y_train, iris_y_test = model_selection.train_test_split(
iris_X,iris_y, test_size =.2)
# create dt,
dt = tree.DecisionTreeClassifier()
# set param grid
params_dt = {'criterion':['gini','entropy'],
'max_depth':[2,3,4,5,6],
'min_samples_leaf':list(range(2,20,2))}
# create optimizer
dt_opt = model_selection.GridSearchCV(dt,params_dt,cv=10)
# optimize the dt parameters
dt_opt.fit(iris_X_train,iris_y_train)
# store the results in a dataframe
dt_df = pd.DataFrame(dt_opt.cv_results_)
# create svm, its parameter grid and optimizer
svm_clf = svm.SVC()
param_grid = {'kernel':['linear','rbf'], 'C':[.5, .75,1,2,5,7, 10]}
svm_opt = model_selection.GridSearchCV(svm_clf,param_grid,cv=10)
# optmize the svm put the CV results in a dataframe
svm_opt.fit(iris_X_train,iris_y_train)
sv_df = pd.DataFrame(svm_opt.cv_results_)
So we have redone some familiar code. We have found the optimal parameters for best accuracy for two different classifiers, SVM and Decision tree on our data.
This is extra detail we did not do in class for time reasons
We can use EDA to understand how the score varied across all of the parameter settings we tried.
sv_df['mean_test_score'].describe()
count 14.000000
mean 0.982143
std 0.005525
min 0.966667
25% 0.983333
50% 0.983333
75% 0.983333
max 0.991667
Name: mean_test_score, dtype: float64
dt_df['mean_test_score'].describe()
count 90.000000
mean 0.947685
std 0.007393
min 0.941667
25% 0.941667
50% 0.950000
75% 0.950000
max 0.975000
Name: mean_test_score, dtype: float64
From this we see that in both cases the standard deviation (std) is really low. This tells us that the parameter changes didn’t impact the performance much. Combined with the overall high accuracy this tells us that the data is probably really easy to classify. If the performance had been uniformly bad, it might have instead told us that we did not try a wide enough range of parameters.
To confirm how many parameter settings we have used we can check a couple different ways. First, above in the count of the describe.
We can also calculate directly from the parameter grids before we even do the fit.
description_vars = ['param_C', 'param_kernel', 'params',]
vars_to_plot = ['mean_fit_time', 'std_fit_time', 'mean_score_time', 'std_score_time']
svm_time = sv_df.melt(id_vars= description_vars,
value_vars=vars_to_plot)
sns.lmplot(data=sv_df, x='mean_fit_time',y='mean_test_score',
hue='param_kernel',fit_reg=False)
<seaborn.axisgrid.FacetGrid at 0x7f34e4e2dd90>
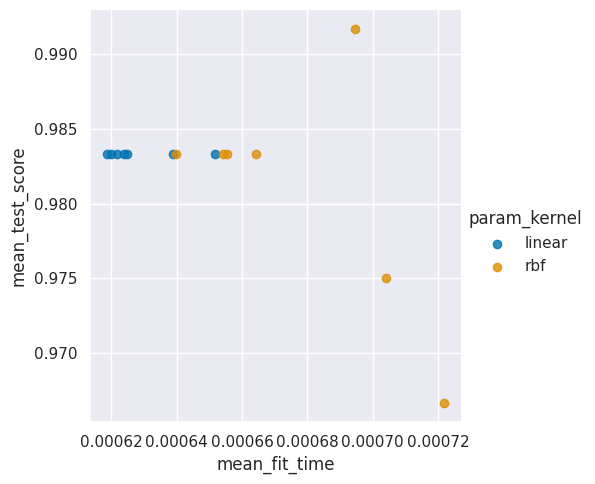
20.1. How does the timing vary?#
Let’s dig in and see which one is better.
sv_df.head(1)
| mean_fit_time | std_fit_time | mean_score_time | std_score_time | param_C | param_kernel | params | split0_test_score | split1_test_score | split2_test_score | split3_test_score | split4_test_score | split5_test_score | split6_test_score | split7_test_score | split8_test_score | split9_test_score | mean_test_score | std_test_score | rank_test_score | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.000652 | 0.000037 | 0.000432 | 0.000012 | 0.5 | linear | {'C': 0.5, 'kernel': 'linear'} | 1.0 | 0.916667 | 1.0 | 1.0 | 1.0 | 0.916667 | 1.0 | 1.0 | 1.0 | 1.0 | 0.983333 | 0.033333 | 2 |
svm_time = sv_df.melt(id_vars=['param_C', 'param_kernel', 'params',],
value_vars=['mean_fit_time', 'std_fit_time', 'mean_score_time', 'std_score_time'])
sns.lmplot(data=sv_df, x='mean_fit_time',y='mean_test_score',
hue='param_kernel',fit_reg=False)
<seaborn.axisgrid.FacetGrid at 0x7f34e4e1ad00>

svm_time.head()
| param_C | param_kernel | params | variable | value | |
|---|---|---|---|---|---|
| 0 | 0.5 | linear | {'C': 0.5, 'kernel': 'linear'} | mean_fit_time | 0.000652 |
| 1 | 0.5 | rbf | {'C': 0.5, 'kernel': 'rbf'} | mean_fit_time | 0.000722 |
| 2 | 0.75 | linear | {'C': 0.75, 'kernel': 'linear'} | mean_fit_time | 0.000619 |
| 3 | 0.75 | rbf | {'C': 0.75, 'kernel': 'rbf'} | mean_fit_time | 0.000704 |
| 4 | 1 | linear | {'C': 1, 'kernel': 'linear'} | mean_fit_time | 0.000620 |
sns.catplot(data= svm_time, x='param_kernel',y='value',hue='variable')
<seaborn.axisgrid.FacetGrid at 0x7f34e298d2b0>
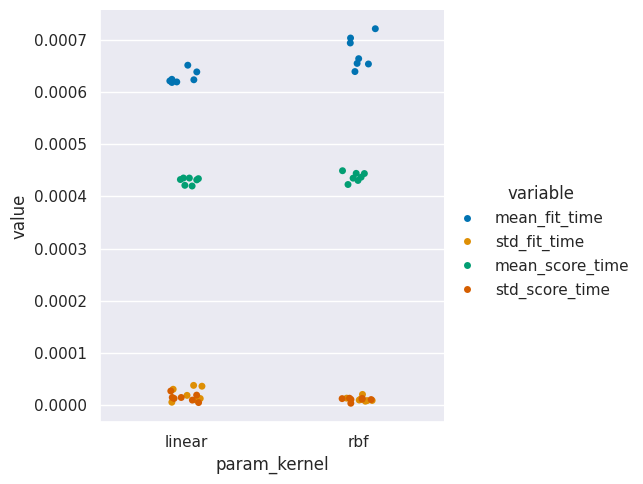
20.2. How does training impact our model?#
Now we can create the learning curve.
train_sizes, train_scores, test_scores, fit_times, score_times = model_selection.learning_curve(svm_opt.best_estimator_,iris_X_train, iris_y_train,
train_sizes= [.4,.5,.6,.8],return_times=True)
It returns the list of the counts for each training size (we input percentages and it returns counts)
[train_sizes, train_scores, test_scores, fit_times, score_times]
[array([38, 48, 57, 76]),
array([[0.92105263, 0.94736842, 0.97368421, 0.97368421, 0.97368421],
[1. , 0.97916667, 0.97916667, 0.97916667, 0.97916667],
[0.94736842, 0.92982456, 0.94736842, 0.98245614, 0.98245614],
[1. , 0.97368421, 0.98684211, 0.98684211, 0.94736842]]),
array([[0.91666667, 0.91666667, 0.95833333, 1. , 1. ],
[0.91666667, 0.95833333, 1. , 1. , 1. ],
[0.91666667, 0.95833333, 0.95833333, 1. , 1. ],
[0.95833333, 1. , 1. , 1. , 1. ]]),
array([[0.00092936, 0.00060821, 0.00060725, 0.00060034, 0.00063634],
[0.00065184, 0.00063157, 0.00061274, 0.00061822, 0.00064993],
[0.00064802, 0.00063062, 0.00065327, 0.00062633, 0.00063324],
[0.00070524, 0.00066423, 0.00066137, 0.00066113, 0.00067663]]),
array([[0.00051999, 0.0004375 , 0.00044537, 0.00045609, 0.00044346],
[0.00046015, 0.0004735 , 0.00044131, 0.00043869, 0.00044417],
[0.00044513, 0.00044847, 0.00044203, 0.00044107, 0.00044894],
[0.00045919, 0.00045323, 0.00045228, 0.00045204, 0.00045347]])]
We can use our skills in transforming data to make it easier to exmine just a subset of the scores.
train_scores.mean(axis=1)
array([0.95789474, 0.98333333, 0.95789474, 0.97894737])
We can stack these into a list, with the means for the cross validated values
[train_sizes, train_scores.mean(axis=1), test_scores.mean(axis=1),
fit_times.mean(axis=1), score_times.mean(axis=1)]
[array([38, 48, 57, 76]),
array([0.95789474, 0.98333333, 0.95789474, 0.97894737]),
array([0.95833333, 0.975 , 0.96666667, 0.99166667]),
array([0.0006763 , 0.00063286, 0.00063829, 0.00067372]),
array([0.00046048, 0.00045156, 0.00044513, 0.00045404])]
then cast it to a numpy array
np.asarray([train_sizes, train_scores.mean(axis=1), test_scores.mean(axis=1),
fit_times.mean(axis=1), score_times.mean(axis=1)]).T
array([[3.80000000e+01, 9.57894737e-01, 9.58333333e-01, 6.76298141e-04,
4.60481644e-04],
[4.80000000e+01, 9.83333333e-01, 9.75000000e-01, 6.32858276e-04,
4.51564789e-04],
[5.70000000e+01, 9.57894737e-01, 9.66666667e-01, 6.38294220e-04,
4.45127487e-04],
[7.60000000e+01, 9.78947368e-01, 9.91666667e-01, 6.73723221e-04,
4.54044342e-04]])
Then we can put it all into a DataFrame so that we can plot it.
curve_df = pd.DataFrame(data = np.asarray([train_sizes, train_scores.mean(axis=1), test_scores.mean(axis=1),
fit_times.mean(axis=1), score_times.mean(axis=1)]).T,
columns = ['train_sizes', 'train_scores', 'test_scores', 'fit_times', 'score_times'])
curve_df.head()
| train_sizes | train_scores | test_scores | fit_times | score_times | |
|---|---|---|---|---|---|
| 0 | 38.0 | 0.957895 | 0.958333 | 0.000676 | 0.000460 |
| 1 | 48.0 | 0.983333 | 0.975000 | 0.000633 | 0.000452 |
| 2 | 57.0 | 0.957895 | 0.966667 | 0.000638 | 0.000445 |
| 3 | 76.0 | 0.978947 | 0.991667 | 0.000674 | 0.000454 |
we will melt it to make it tidy and can work better with seaborn plotting functions.
curve_df_tall = curve_df.melt(id_vars='train_sizes',)
sns.relplot(data =curve_df_tall,x='train_sizes',y ='value',hue ='variable' )
<seaborn.axisgrid.FacetGrid at 0x7f34e28a5e80>
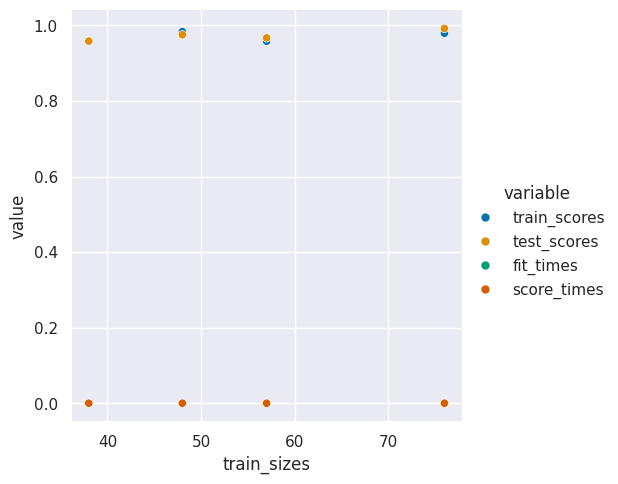
We can see here that the training score and test score are basically the same. This means we’re doing about as well as we cana at learning the a generalizable model and we probably hav enough data for this task.
20.3. Digits Dataset#
Today, we’ll load a new dataset and use the default sklearn data structure for datasets. We get back the default data stucture when we use a load_ function without any parameters at all.
digits = datasets.load_digits()
This shows us that the type is defined by sklearn and they called it bunch:
type(digits)
sklearn.utils._bunch.Bunch
We can print it out to begin exploring it.
digits
{'data': array([[ 0., 0., 5., ..., 0., 0., 0.],
[ 0., 0., 0., ..., 10., 0., 0.],
[ 0., 0., 0., ..., 16., 9., 0.],
...,
[ 0., 0., 1., ..., 6., 0., 0.],
[ 0., 0., 2., ..., 12., 0., 0.],
[ 0., 0., 10., ..., 12., 1., 0.]]),
'target': array([0, 1, 2, ..., 8, 9, 8]),
'frame': None,
'feature_names': ['pixel_0_0',
'pixel_0_1',
'pixel_0_2',
'pixel_0_3',
'pixel_0_4',
'pixel_0_5',
'pixel_0_6',
'pixel_0_7',
'pixel_1_0',
'pixel_1_1',
'pixel_1_2',
'pixel_1_3',
'pixel_1_4',
'pixel_1_5',
'pixel_1_6',
'pixel_1_7',
'pixel_2_0',
'pixel_2_1',
'pixel_2_2',
'pixel_2_3',
'pixel_2_4',
'pixel_2_5',
'pixel_2_6',
'pixel_2_7',
'pixel_3_0',
'pixel_3_1',
'pixel_3_2',
'pixel_3_3',
'pixel_3_4',
'pixel_3_5',
'pixel_3_6',
'pixel_3_7',
'pixel_4_0',
'pixel_4_1',
'pixel_4_2',
'pixel_4_3',
'pixel_4_4',
'pixel_4_5',
'pixel_4_6',
'pixel_4_7',
'pixel_5_0',
'pixel_5_1',
'pixel_5_2',
'pixel_5_3',
'pixel_5_4',
'pixel_5_5',
'pixel_5_6',
'pixel_5_7',
'pixel_6_0',
'pixel_6_1',
'pixel_6_2',
'pixel_6_3',
'pixel_6_4',
'pixel_6_5',
'pixel_6_6',
'pixel_6_7',
'pixel_7_0',
'pixel_7_1',
'pixel_7_2',
'pixel_7_3',
'pixel_7_4',
'pixel_7_5',
'pixel_7_6',
'pixel_7_7'],
'target_names': array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9]),
'images': array([[[ 0., 0., 5., ..., 1., 0., 0.],
[ 0., 0., 13., ..., 15., 5., 0.],
[ 0., 3., 15., ..., 11., 8., 0.],
...,
[ 0., 4., 11., ..., 12., 7., 0.],
[ 0., 2., 14., ..., 12., 0., 0.],
[ 0., 0., 6., ..., 0., 0., 0.]],
[[ 0., 0., 0., ..., 5., 0., 0.],
[ 0., 0., 0., ..., 9., 0., 0.],
[ 0., 0., 3., ..., 6., 0., 0.],
...,
[ 0., 0., 1., ..., 6., 0., 0.],
[ 0., 0., 1., ..., 6., 0., 0.],
[ 0., 0., 0., ..., 10., 0., 0.]],
[[ 0., 0., 0., ..., 12., 0., 0.],
[ 0., 0., 3., ..., 14., 0., 0.],
[ 0., 0., 8., ..., 16., 0., 0.],
...,
[ 0., 9., 16., ..., 0., 0., 0.],
[ 0., 3., 13., ..., 11., 5., 0.],
[ 0., 0., 0., ..., 16., 9., 0.]],
...,
[[ 0., 0., 1., ..., 1., 0., 0.],
[ 0., 0., 13., ..., 2., 1., 0.],
[ 0., 0., 16., ..., 16., 5., 0.],
...,
[ 0., 0., 16., ..., 15., 0., 0.],
[ 0., 0., 15., ..., 16., 0., 0.],
[ 0., 0., 2., ..., 6., 0., 0.]],
[[ 0., 0., 2., ..., 0., 0., 0.],
[ 0., 0., 14., ..., 15., 1., 0.],
[ 0., 4., 16., ..., 16., 7., 0.],
...,
[ 0., 0., 0., ..., 16., 2., 0.],
[ 0., 0., 4., ..., 16., 2., 0.],
[ 0., 0., 5., ..., 12., 0., 0.]],
[[ 0., 0., 10., ..., 1., 0., 0.],
[ 0., 2., 16., ..., 1., 0., 0.],
[ 0., 0., 15., ..., 15., 0., 0.],
...,
[ 0., 4., 16., ..., 16., 6., 0.],
[ 0., 8., 16., ..., 16., 8., 0.],
[ 0., 1., 8., ..., 12., 1., 0.]]]),
'DESCR': ".. _digits_dataset:\n\nOptical recognition of handwritten digits dataset\n--------------------------------------------------\n\n**Data Set Characteristics:**\n\n :Number of Instances: 1797\n :Number of Attributes: 64\n :Attribute Information: 8x8 image of integer pixels in the range 0..16.\n :Missing Attribute Values: None\n :Creator: E. Alpaydin (alpaydin '@' boun.edu.tr)\n :Date: July; 1998\n\nThis is a copy of the test set of the UCI ML hand-written digits datasets\nhttps://archive.ics.uci.edu/ml/datasets/Optical+Recognition+of+Handwritten+Digits\n\nThe data set contains images of hand-written digits: 10 classes where\neach class refers to a digit.\n\nPreprocessing programs made available by NIST were used to extract\nnormalized bitmaps of handwritten digits from a preprinted form. From a\ntotal of 43 people, 30 contributed to the training set and different 13\nto the test set. 32x32 bitmaps are divided into nonoverlapping blocks of\n4x4 and the number of on pixels are counted in each block. This generates\nan input matrix of 8x8 where each element is an integer in the range\n0..16. This reduces dimensionality and gives invariance to small\ndistortions.\n\nFor info on NIST preprocessing routines, see M. D. Garris, J. L. Blue, G.\nT. Candela, D. L. Dimmick, J. Geist, P. J. Grother, S. A. Janet, and C.\nL. Wilson, NIST Form-Based Handprint Recognition System, NISTIR 5469,\n1994.\n\n|details-start|\n**References**\n|details-split|\n\n- C. Kaynak (1995) Methods of Combining Multiple Classifiers and Their\n Applications to Handwritten Digit Recognition, MSc Thesis, Institute of\n Graduate Studies in Science and Engineering, Bogazici University.\n- E. Alpaydin, C. Kaynak (1998) Cascading Classifiers, Kybernetika.\n- Ken Tang and Ponnuthurai N. Suganthan and Xi Yao and A. Kai Qin.\n Linear dimensionalityreduction using relevance weighted LDA. School of\n Electrical and Electronic Engineering Nanyang Technological University.\n 2005.\n- Claudio Gentile. A New Approximate Maximal Margin Classification\n Algorithm. NIPS. 2000.\n\n|details-end|"}
We note that it has key value pairs, and that the last one is called DESCR and is text that describes the data. If we send that to the print function it will be formatted more readably.
print(digits['DESCR'])
.. _digits_dataset:
Optical recognition of handwritten digits dataset
--------------------------------------------------
**Data Set Characteristics:**
:Number of Instances: 1797
:Number of Attributes: 64
:Attribute Information: 8x8 image of integer pixels in the range 0..16.
:Missing Attribute Values: None
:Creator: E. Alpaydin (alpaydin '@' boun.edu.tr)
:Date: July; 1998
This is a copy of the test set of the UCI ML hand-written digits datasets
https://archive.ics.uci.edu/ml/datasets/Optical+Recognition+of+Handwritten+Digits
The data set contains images of hand-written digits: 10 classes where
each class refers to a digit.
Preprocessing programs made available by NIST were used to extract
normalized bitmaps of handwritten digits from a preprinted form. From a
total of 43 people, 30 contributed to the training set and different 13
to the test set. 32x32 bitmaps are divided into nonoverlapping blocks of
4x4 and the number of on pixels are counted in each block. This generates
an input matrix of 8x8 where each element is an integer in the range
0..16. This reduces dimensionality and gives invariance to small
distortions.
For info on NIST preprocessing routines, see M. D. Garris, J. L. Blue, G.
T. Candela, D. L. Dimmick, J. Geist, P. J. Grother, S. A. Janet, and C.
L. Wilson, NIST Form-Based Handprint Recognition System, NISTIR 5469,
1994.
|details-start|
**References**
|details-split|
- C. Kaynak (1995) Methods of Combining Multiple Classifiers and Their
Applications to Handwritten Digit Recognition, MSc Thesis, Institute of
Graduate Studies in Science and Engineering, Bogazici University.
- E. Alpaydin, C. Kaynak (1998) Cascading Classifiers, Kybernetika.
- Ken Tang and Ponnuthurai N. Suganthan and Xi Yao and A. Kai Qin.
Linear dimensionalityreduction using relevance weighted LDA. School of
Electrical and Electronic Engineering Nanyang Technological University.
2005.
- Claudio Gentile. A New Approximate Maximal Margin Classification
Algorithm. NIPS. 2000.
|details-end|
This tells us that we are going to be predicting what digit (0,1,2,3,4,5,6,7,8, or 9) is in the image.
To get an idea of what the images look like, we can use matshow which is short for matrix show. It takes a 2D matrix and plots it as a grayscale image. To get the actual color bar, we use the matplotlib plt.gray().
plt.gray()
plt.matshow(digits.images[8])
<matplotlib.image.AxesImage at 0x7f34e27a32b0>
<Figure size 640x480 with 0 Axes>
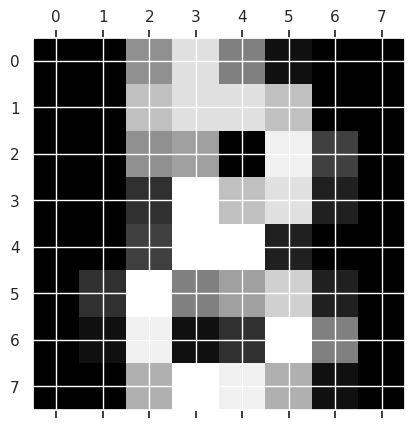
and we can pick another one
plt.gray()
plt.matshow(digits.images[198])
<matplotlib.image.AxesImage at 0x7f34e272afa0>
<Figure size 640x480 with 0 Axes>
For easier ML, we will reload it differently:
digits_X, digits_y = datasets.load_digits(return_X_y=True)
This has one row for each sample and has reshaped the 8x8 image into a 64 length vector. So we have one ‘feature’ for each pixel in the images.
digits_X.shape
(1797, 64)
Now we can train a model and generate a learning curve.
svm_clf_digits = svm.SVC()
train_sizes, train_scores, test_scores, fit_times, score_times = model_selection.learning_curve(
svm_clf_digits,digits_X, digits_y,
train_sizes= [.1,.2,.3,.4,.5,.6,.8,.9, .95,.97,.99],return_times=True)
and we will make this into a DataFrame the same way as with the iris data above.
digits_curve_df = pd.DataFrame(data = np.asarray([train_sizes, train_scores.mean(axis=1), test_scores.mean(axis=1),
fit_times.mean(axis=1), score_times.mean(axis=1)]).T,
columns = ['train_sizes', 'train_scores', 'test_scores', 'fit_times', 'score_times'])
digits_curve_df
| train_sizes | train_scores | test_scores | fit_times | score_times | |
|---|---|---|---|---|---|
| 0 | 143.0 | 0.991608 | 0.817487 | 0.002587 | 0.004109 |
| 1 | 287.0 | 0.993031 | 0.855317 | 0.004158 | 0.005329 |
| 2 | 431.0 | 0.998144 | 0.906541 | 0.006462 | 0.007242 |
| 3 | 574.0 | 0.996167 | 0.932690 | 0.009223 | 0.008924 |
| 4 | 718.0 | 0.998886 | 0.942696 | 0.012506 | 0.010505 |
| 5 | 862.0 | 0.996984 | 0.948813 | 0.015840 | 0.011988 |
| 6 | 1149.0 | 0.997041 | 0.957722 | 0.022564 | 0.014006 |
| 7 | 1293.0 | 0.997525 | 0.959947 | 0.027328 | 0.015204 |
| 8 | 1365.0 | 0.996923 | 0.962730 | 0.029340 | 0.015896 |
| 9 | 1393.0 | 0.997128 | 0.962728 | 0.030480 | 0.016153 |
| 10 | 1422.0 | 0.997046 | 0.962171 | 0.031185 | 0.016165 |
digits_curve_df_tall = digits_curve_df.melt(id_vars = 'train_sizes', value_vars=[ 'train_scores', 'test_scores'])
sns.relplot(data =digits_curve_df_tall, x = 'train_sizes',y='value',hue='variable',)
<seaborn.axisgrid.FacetGrid at 0x7f34e26f8b50>
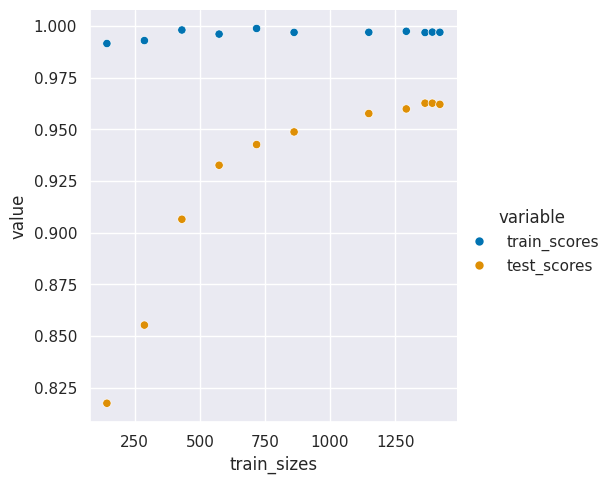
This larger gap shows that a different model or maybe more data could help us learn better. Th good news is that we are probably not overfitting, overfitting would occur when the training accuracy still improves but the test accuracy goes down.
20.4. Decision Tree with digits data#
dt_digits = tree.DecisionTreeClassifier()
train_sizes, train_scores, test_scores, fit_times, score_times = model_selection.learning_curve(
dt_digits,digits_X, digits_y,
train_sizes= [.1,.2,.3,.4,.5,.6,.8,.9, .95,.97,.99],return_times=True)
train_scores.shape
(11, 5)
digits_curve_df_dt = pd.DataFrame(data = np.asarray([train_sizes, train_scores.mean(axis=1), test_scores.mean(axis=1),
fit_times.mean(axis=1), score_times.mean(axis=1)]).T,
columns = ['train_sizes', 'train_scores', 'test_scores', 'fit_times', 'score_times'])
digits_curve_df_dt
| train_sizes | train_scores | test_scores | fit_times | score_times | |
|---|---|---|---|---|---|
| 0 | 143.0 | 1.0 | 0.523109 | 0.001890 | 0.000509 |
| 1 | 287.0 | 1.0 | 0.562609 | 0.003171 | 0.000504 |
| 2 | 431.0 | 1.0 | 0.652221 | 0.004621 | 0.000497 |
| 3 | 574.0 | 1.0 | 0.714005 | 0.006094 | 0.000537 |
| 4 | 718.0 | 1.0 | 0.693957 | 0.007682 | 0.000507 |
| 5 | 862.0 | 1.0 | 0.732357 | 0.009832 | 0.000500 |
| 6 | 1149.0 | 1.0 | 0.776888 | 0.012870 | 0.000558 |
| 7 | 1293.0 | 1.0 | 0.782417 | 0.014844 | 0.000612 |
| 8 | 1365.0 | 1.0 | 0.778548 | 0.016115 | 0.000559 |
| 9 | 1393.0 | 1.0 | 0.792453 | 0.016198 | 0.000515 |
| 10 | 1422.0 | 1.0 | 0.789123 | 0.016324 | 0.000605 |
digits_curve_df_tall_dt = digits_curve_df_dt.melt(id_vars = 'train_sizes', value_vars=[ 'train_scores', 'test_scores'])
sns.relplot(data =digits_curve_df_tall_dt, x = 'train_sizes',y='value',hue='variable',)
<seaborn.axisgrid.FacetGrid at 0x7f34e2623c40>
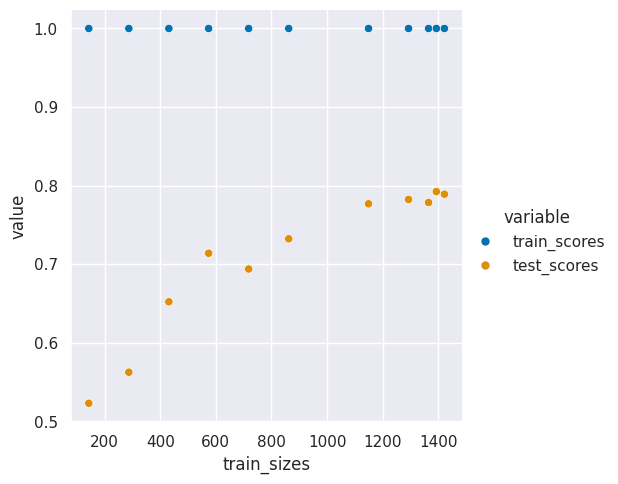
This one does much worse that above.
Important
I spent time also giving help and answering questions for A11.
