23. Neural Networks#
23.1. Admin#
Important
We will have 2 speakers to wrap up the semester:
12/7: Nirmal Keshava
12/12: Tiffany Sithiphone
Note
P3 is due 12/4 unless you got a note from me saying that I saw your P2, but I have not graded it yet.
23.2. What is a Neural Network#
We started thinking about machine learning with the idea that the basic idea is that we assume that our target variable (\(y_i\)) is related to the features \(\mathbf{x}_i\) by some function (for sample \(i\)):
But we don’t know that function exactly, so we assume a type (a decision tree, a boundary for SVM, a probability distribution) that has some parameters \(\theta\) and then use a machine learning algorithm \(\mathcal{A}\) to estimate the parameters for \(f\). In the decision tree the parameters are the thresholds to compare to, in the GaussianNB the parameters are the mean and variance, in SVM it’s the support vectors that define the margin.
That we can use to test on our test data:
A neural net allows us to not assume a specific form for \(f\) first, it does universal function approximation. For one hidden layer and a binary classification problem:
where the function \(g\) is called the activation function. We approximate some unknown, complicated function \(f\) by taking a weighted sum of all of the inputs, and passing those through another, known function, \(g\).
The learning step involves finding the weights and biases (or coeffificents and intercepts). It does so by finding the weights that minimize some loss function on the data:
where the loss function \(\ell\) describes the “cost” of errors. For example it might be simple does the prediction match or more complex like how close it is.
23.3. NN in Sklearn#
from scipy.special import expit
from sklearn.datasets import make_classification
from sklearn.neural_network import MLPClassifier
from sklearn import svm
import pandas as pd
import numpy as np
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn import model_selection
from sklearn.model_selection import train_test_split
import seaborn as sns
sns.set_theme(palette='colorblind')
We will use the digits dataset again.
digits = datasets.load_digits()
digits_X = digits.data
digits_y = digits.target
X_train, X_test, y_train, y_test = model_selection.train_test_split(digits_X,digits_y)
digits.images[0]
array([[ 0., 0., 5., 13., 9., 1., 0., 0.],
[ 0., 0., 13., 15., 10., 15., 5., 0.],
[ 0., 3., 15., 2., 0., 11., 8., 0.],
[ 0., 4., 12., 0., 0., 8., 8., 0.],
[ 0., 5., 8., 0., 0., 9., 8., 0.],
[ 0., 4., 11., 0., 1., 12., 7., 0.],
[ 0., 2., 14., 5., 10., 12., 0., 0.],
[ 0., 0., 6., 13., 10., 0., 0., 0.]])
sklearn provides a neural network by the name MLPClassifier
mlp = MLPClassifier(
hidden_layer_sizes=(16),
max_iter=100,
solver="lbfgs",
verbose=10,
random_state=1,
learning_rate_init=0.1,
)
We specify:
the number of neurons in each hidden layer
the number of steps in the optimizaiton to do
the solver is the algorithm used to find the parameters
for it to output interim info as it works
fix the random state so we all use the same initialization
the initial learning rate (how fast to change parameter values while searching)
Then we use it just like we use all other sklearn estimators.
mlp.fit(X_train, y_train).score(X_test,y_test)
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 1210 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 9.40391D+00 |proj g|= 7.25043D+00
At iterate 1 f= 8.27245D+00 |proj g|= 7.33800D+00
At iterate 2 f= 3.34677D+00 |proj g|= 2.06114D+00
At iterate 3 f= 2.40712D+00 |proj g|= 4.15820D-01
At iterate 4 f= 2.29097D+00 |proj g|= 2.54784D-01
At iterate 5 f= 2.13910D+00 |proj g|= 2.77693D-01
At iterate 6 f= 2.01280D+00 |proj g|= 2.89541D-01
At iterate 7 f= 1.72508D+00 |proj g|= 1.01612D+00
At iterate 8 f= 1.65968D+00 |proj g|= 6.66645D-01
At iterate 9 f= 1.54443D+00 |proj g|= 3.46057D-01
At iterate 10 f= 1.48358D+00 |proj g|= 3.27554D-01
At iterate 11 f= 1.41171D+00 |proj g|= 2.85272D-01
At iterate 12 f= 1.23456D+00 |proj g|= 2.73880D-01
At iterate 13 f= 1.17939D+00 |proj g|= 9.80296D-01
At iterate 14 f= 1.10448D+00 |proj g|= 2.47666D-01
At iterate 15 f= 1.07770D+00 |proj g|= 1.56778D-01
At iterate 16 f= 1.01970D+00 |proj g|= 4.87342D-01
At iterate 17 f= 9.78778D-01 |proj g|= 4.73049D-01
At iterate 18 f= 9.26638D-01 |proj g|= 2.03028D-01
At iterate 19 f= 8.76803D-01 |proj g|= 2.02681D-01
At iterate 20 f= 8.27339D-01 |proj g|= 4.31792D-01
At iterate 21 f= 7.68534D-01 |proj g|= 4.63986D-01
At iterate 22 f= 7.41465D-01 |proj g|= 2.76490D-01
At iterate 23 f= 7.26458D-01 |proj g|= 1.33532D-01
At iterate 24 f= 7.04734D-01 |proj g|= 2.71124D-01
At iterate 25 f= 6.75241D-01 |proj g|= 3.87226D-01
At iterate 26 f= 6.42634D-01 |proj g|= 1.70220D-01
At iterate 27 f= 6.10969D-01 |proj g|= 4.69950D-01
At iterate 28 f= 5.79995D-01 |proj g|= 3.94014D-01
At iterate 29 f= 5.48411D-01 |proj g|= 3.69173D-01
At iterate 30 f= 5.12923D-01 |proj g|= 4.76438D-01
At iterate 31 f= 4.79564D-01 |proj g|= 1.44522D-01
At iterate 32 f= 4.60730D-01 |proj g|= 2.33291D-01
At iterate 33 f= 4.45106D-01 |proj g|= 1.08693D-01
At iterate 34 f= 4.18274D-01 |proj g|= 4.12410D-01
At iterate 35 f= 4.00504D-01 |proj g|= 2.83697D-01
At iterate 36 f= 3.80351D-01 |proj g|= 1.02830D-01
At iterate 37 f= 3.56491D-01 |proj g|= 1.35042D-01
At iterate 38 f= 3.36476D-01 |proj g|= 2.00188D-01
At iterate 39 f= 3.23757D-01 |proj g|= 5.98133D-01
At iterate 40 f= 3.06646D-01 |proj g|= 1.81957D-01
At iterate 41 f= 3.01625D-01 |proj g|= 9.67825D-02
At iterate 42 f= 2.93063D-01 |proj g|= 5.24219D-02
At iterate 43 f= 2.75103D-01 |proj g|= 1.50304D-01
At iterate 44 f= 2.63878D-01 |proj g|= 2.86373D-01
At iterate 45 f= 2.49254D-01 |proj g|= 9.18127D-02
At iterate 46 f= 2.42015D-01 |proj g|= 7.12341D-02
At iterate 47 f= 2.37280D-01 |proj g|= 8.79295D-02
At iterate 48 f= 2.26173D-01 |proj g|= 1.09953D-01
At iterate 49 f= 2.24209D-01 |proj g|= 2.51448D-01
At iterate 50 f= 2.15664D-01 |proj g|= 6.69376D-02
At iterate 51 f= 2.11250D-01 |proj g|= 3.67292D-02
At iterate 52 f= 2.04076D-01 |proj g|= 9.44192D-02
At iterate 53 f= 1.95835D-01 |proj g|= 1.56955D-01
At iterate 54 f= 1.92756D-01 |proj g|= 1.88308D-01
At iterate 55 f= 1.85303D-01 |proj g|= 3.87196D-02
At iterate 56 f= 1.82619D-01 |proj g|= 6.74958D-02
At iterate 57 f= 1.76912D-01 |proj g|= 1.13160D-01
At iterate 58 f= 1.72024D-01 |proj g|= 1.20778D-01
At iterate 59 f= 1.67015D-01 |proj g|= 3.51875D-02
At iterate 60 f= 1.63303D-01 |proj g|= 7.03249D-02
At iterate 61 f= 1.60459D-01 |proj g|= 7.64248D-02
At iterate 62 f= 1.55862D-01 |proj g|= 3.82312D-02
At iterate 63 f= 1.55102D-01 |proj g|= 1.72817D-01
At iterate 64 f= 1.52024D-01 |proj g|= 7.05391D-02
At iterate 65 f= 1.50135D-01 |proj g|= 3.15599D-02
At iterate 66 f= 1.47715D-01 |proj g|= 7.04390D-02
At iterate 67 f= 1.45089D-01 |proj g|= 8.60698D-02
At iterate 68 f= 1.41113D-01 |proj g|= 6.55423D-02
At iterate 69 f= 1.38332D-01 |proj g|= 9.10053D-02
At iterate 70 f= 1.35825D-01 |proj g|= 4.06173D-02
At iterate 71 f= 1.32371D-01 |proj g|= 6.01693D-02
At iterate 72 f= 1.30045D-01 |proj g|= 6.52722D-02
At iterate 73 f= 1.27703D-01 |proj g|= 3.93364D-02
At iterate 74 f= 1.26034D-01 |proj g|= 4.53927D-02
At iterate 75 f= 1.21125D-01 |proj g|= 6.18286D-02
At iterate 76 f= 1.18190D-01 |proj g|= 5.74455D-02
At iterate 77 f= 1.15610D-01 |proj g|= 2.68655D-02
At iterate 78 f= 1.13272D-01 |proj g|= 2.64427D-02
At iterate 79 f= 1.11289D-01 |proj g|= 4.45123D-02
At iterate 80 f= 1.09776D-01 |proj g|= 7.84298D-02
At iterate 81 f= 1.08314D-01 |proj g|= 4.59670D-02
At iterate 82 f= 1.06905D-01 |proj g|= 3.35440D-02
At iterate 83 f= 1.05637D-01 |proj g|= 4.30825D-02
At iterate 84 f= 1.03096D-01 |proj g|= 6.32154D-02
At iterate 85 f= 1.00656D-01 |proj g|= 7.66120D-02
At iterate 86 f= 9.92600D-02 |proj g|= 3.20820D-02
At iterate 87 f= 9.78231D-02 |proj g|= 3.00969D-02
At iterate 88 f= 9.65266D-02 |proj g|= 4.26389D-02
At iterate 89 f= 9.52018D-02 |proj g|= 4.81253D-02
At iterate 90 f= 9.34543D-02 |proj g|= 4.91024D-02
At iterate 91 f= 9.18389D-02 |proj g|= 2.82063D-02
At iterate 92 f= 9.05110D-02 |proj g|= 2.93229D-02
At iterate 93 f= 8.87077D-02 |proj g|= 3.85490D-02
At iterate 94 f= 8.56893D-02 |proj g|= 7.31366D-02
At iterate 95 f= 8.44146D-02 |proj g|= 2.11226D-02
At iterate 96 f= 8.39004D-02 |proj g|= 1.98654D-02
At iterate 97 f= 8.22351D-02 |proj g|= 2.69318D-02
At iterate 98 f= 8.12596D-02 |proj g|= 4.30663D-02
At iterate 99 f= 7.98023D-02 |proj g|= 7.89129D-02
At iterate 100 f= 7.83888D-02 |proj g|= 2.82801D-02
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
1210 100 104 1 0 0 2.828D-02 7.839D-02
F = 7.8388839659254791E-002
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT
This problem is unconstrained.
/opt/hostedtoolcache/Python/3.8.18/x64/lib/python3.8/site-packages/sklearn/neural_network/_multilayer_perceptron.py:546: ConvergenceWarning: lbfgs failed to converge (status=1):
STOP: TOTAL NO. of ITERATIONS REACHED LIMIT.
Increase the number of iterations (max_iter) or scale the data as shown in:
https://scikit-learn.org/stable/modules/preprocessing.html
self.n_iter_ = _check_optimize_result("lbfgs", opt_res, self.max_iter)
0.9155555555555556
23.4. Comparing nn to mlp#
Letsw fit an SVM
svm_clf = svm.SVC(gamma=0.001)
svm_clf.fit(X_train, y_train)
svm_clf.score(X_test,y_test)
0.9933333333333333
Here we get better performance with this, but we can alos check the complexity to compare them.
We can see how many support vectors that this had to store.
svm_clf.support_vectors_.shape
(691, 64)
and then multiply all together to get the total numbers stored:
np.prod(list(svm_clf.support_vectors_.shape))
44224
for the MLP, we’ll use the weights:
np.sum([np.prod(list(c.shape)) for c in mlp.coefs_])
1184
We can see these shapes are determined by the data and the size of the hidden that we specifies and the number of classes.
[list(c.shape) for c in mlp.coefs_]
[[64, 16], [16, 10]]
In this case we have:
64 features (8x8 pixels)
16 hidden layer neurons
10 classes
we have 10 neurons in the output layer because each output neuron is related to one class. Each output neuron relates to one class, so for it to be one that class is predicted and the others are 0 for training. At prediction time, we say the highest value one is the ones that we read as the prediction. We interpret the outpus as the probability that the sample belongs to each class.
23.5. Neural Network Predictions#
We’ll start with some toy data for classification.
X, y = make_classification(n_samples=100, random_state=1,n_features=2,n_redundant=0)
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, stratify=y,
random_state=1)
sns.scatterplot(x=X[:,0],y=X[:,1],hue=y)
<Axes: >
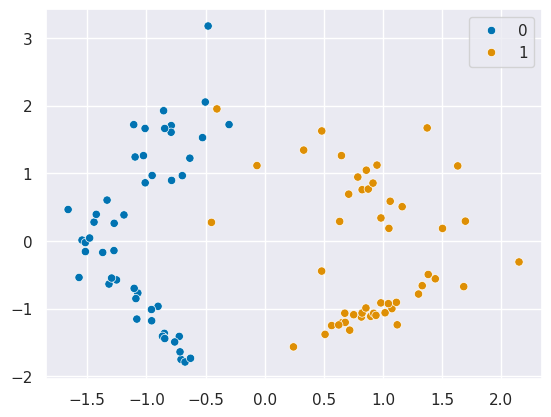
it’s two simple features.
clf = MLPClassifier(
hidden_layer_sizes=(1), # 1 hidden layer, 1 aritficial neuron
max_iter=100, # maximum 100 interations in optimization
alpha=1e-4, # regularization
solver="lbfgs", #optimization algorithm
verbose=10, # how much detail to print
activation= 'identity' # how to transform the hidden layer beofore passing it to the next layer
)
clf.fit(X_train, y_train)
clf.score(X_test, y_test)
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 5 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 8.02331D-01 |proj g|= 5.09797D-01
At iterate 1 f= 3.69278D-01 |proj g|= 2.51074D-01
At iterate 2 f= 1.50478D-01 |proj g|= 8.61969D-02
At iterate 3 f= 9.54380D-02 |proj g|= 4.96103D-02
At iterate 4 f= 7.22965D-02 |proj g|= 2.57521D-02
At iterate 5 f= 6.07288D-02 |proj g|= 1.61252D-02
At iterate 6 f= 5.62998D-02 |proj g|= 2.90812D-02
At iterate 7 f= 5.20850D-02 |proj g|= 1.02569D-02
At iterate 8 f= 4.90884D-02 |proj g|= 2.76414D-03
At iterate 9 f= 4.82053D-02 |proj g|= 3.08878D-03
At iterate 10 f= 4.79256D-02 |proj g|= 7.83441D-04
At iterate 11 f= 4.79062D-02 |proj g|= 9.58952D-05
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments ex
This problem is unconstrained.
1.0
plored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
5 11 12 1 0 0 9.590D-05 4.791D-02
F = 4.7906199858129855E-002
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
this does very well
We can see that this network has one activation for the hidden layers
clf.activation
'identity'
and a different one for the output layer.
clf.out_activation_
'logistic'
The sigmoid function looks like this:
x_logistic = np.linspace(-10,10,100)
y_logistic = expit(x_logistic)
plt.plot(x_logistic,y_logistic)
[<matplotlib.lines.Line2D at 0x7f3b18cffe50>]
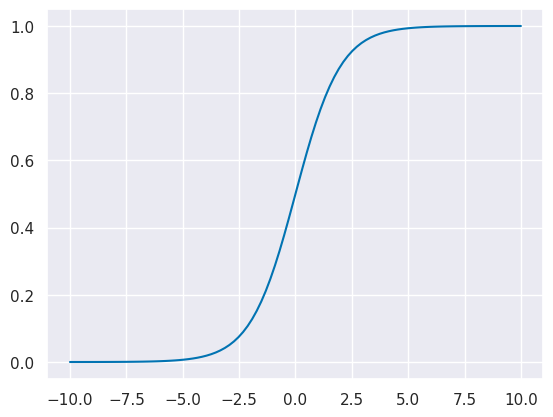
The object also has coefficients
clf.coefs_
[array([[ 4.7401027 ],
[-0.13595873]]),
array([[2.76359301]])]
and intercepts as attributes.
clf.intercepts_
[array([1.8565197]), array([0.54548524])]
To test this, we will make a new sample, the point (-1,2)
pt = np.array([[-1,2]])
The hidden neuron in this case does the following calculation:
np.matmul(pt,clf.coefs_[0]) + clf.intercepts_[0]
array([[-3.15550046]])
then the output neuron takes that as input and uses its own weights, and the sigmoid function
expit((np.matmul(pt,clf.coefs_[0]) + clf.intercepts_[0])*clf.coefs_[1] +clf.intercepts_[1])
array([[0.00028152]])
This calculates the probability the output is 1.
clf.predict_proba(pt)
array([[9.99718482e-01, 2.81517668e-04]])
This method predicts the probabity of both 0 and 1.
1- expit((np.matmul(pt,clf.coefs_[0]) + clf.intercepts_[0])*clf.coefs_[1] +clf.intercepts_[1])
array([[0.99971848]])
and we can confirm that we have replicated the function of the predictions for the neural network.
23.6. Another way to replicate#
We can consider a neuron like a tempalte function:
def aritificial_neuron_template(activation,weights,bias,inputs):
'''
simple artificial neuron
Parameters
----------
activation : function
activation function of the neuron
weights : numpy aray
wights for summing inputs one per input
bias: numpy array
bias term added to the weighted sum
inputs : numpy array
input to the neuron, must be same size as weights
'''
return activation(np.matmul(inputs,weights) +bias)
# two common activation functions
identity_activation = lambda x: x
logistic_activation = lambda x: expit(x)
Notice that this function takes in:
inputs (features)
weights
bias
activation function
We also define two activation functions.
When we set up to train a neural network, we tell the learning algorithm what activation function to use and then it learns the weights.
This is equivalent to our neural network above:
hidden_neuron = lambda x: aritificial_neuron_template(identity_activation,clf.coefs_[0],clf.intercepts_[0],x)
output_neuron = lambda h: aritificial_neuron_template(expit,clf.coefs_[1],clf.intercepts_[1],h)
output_neuron(hidden_neuron(pt))
array([[0.00028152]])
23.7. A more complicated example#
This time we’ll make similar data with 4 features instead of 2 and we’ll set up a test point pt_4d
X, y = make_classification(n_samples=200, random_state=1,n_features=4,n_redundant=0,n_informative=4)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y,
random_state=5)
pt_4d =np.asarray([[-1,-2,2,-1],[1.5,0,.5,1]])
clf_4d = MLPClassifier(
hidden_layer_sizes=(1),
max_iter=5000,
alpha=1e-4,
solver="lbfgs",
verbose=10,
activation= 'identity'
)
clf_4d.fit(X_train, y_train)
clf_4d.score(X_test, y_test)
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 7 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 6.79422D-01 |proj g|= 1.34972D-01
At iterate 1 f= 6.65530D-01 |proj g|= 7.00821D-02
At iterate 2 f= 6.33021D-01 |proj g|= 1.51025D-01
At iterate 3 f= 5.71749D-01 |proj g|= 4.71791D-01
At iterate 4 f= 5.23813D-01 |proj g|= 8.81233D-02
At iterate 5 f= 5.12066D-01 |proj g|= 6.99840D-02
At iterate 6 f= 4.85893D-01 |proj g|= 1.02977D-01
At iterate 7 f= 4.76397D-01 |proj g|= 8.22339D-02
At iterate 8 f= 4.73793D-01 |proj g|= 1.85566D-02
At iterate 9 f= 4.73386D-01 |proj g|= 1.91639D-02
At iterate 10 f= 4.72211D-01 |proj g|= 2.99922D-02
At iterate 11 f= 4.68997D-01 |proj g|= 6.37131D-02
At iterate 12 f= 4.59284D-01 |proj g|= 5.50552D-02
At iterate 13 f= 4.54418D-01 |proj g|= 3.66207D-02
At iterate 14 f= 4.47827D-01 |proj g|= 5.20024D-02
At iterate 15 f= 4.36195D-01 |proj g|= 1.98149D-02
At iterate 16 f= 4.35486D-01 |proj g|= 6.59890D-03
At iterate 17 f= 4.35104D-01 |proj g|= 8.46506D-03
At iterate 18 f= 4.34937D-01 |proj g|= 8.32958D-03
At iterate 19 f= 4.34911D-01 |proj g|= 1.75302D-02
At iterate 20 f= 4.34713D-01 |proj g|= 8.86609D-03
At iterate 21 f= 4.34664D-01 |proj g|= 1.25730D-03
At iterate 22 f= 4.34663D-01 |proj g|= 5.49466D-05
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
7 22 27 1 0 0 5.495D-05 4.347D-01
F = 0.43466279898568450
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
This problem is unconstrained.
0.84
this does well again
we can see the data:
df = pd.DataFrame(X,columns=['x0','x1','x2','x3'])
df['y'] = y
sns.pairplot(df,hue='y')
<seaborn.axisgrid.PairGrid at 0x7f3b18c617f0>
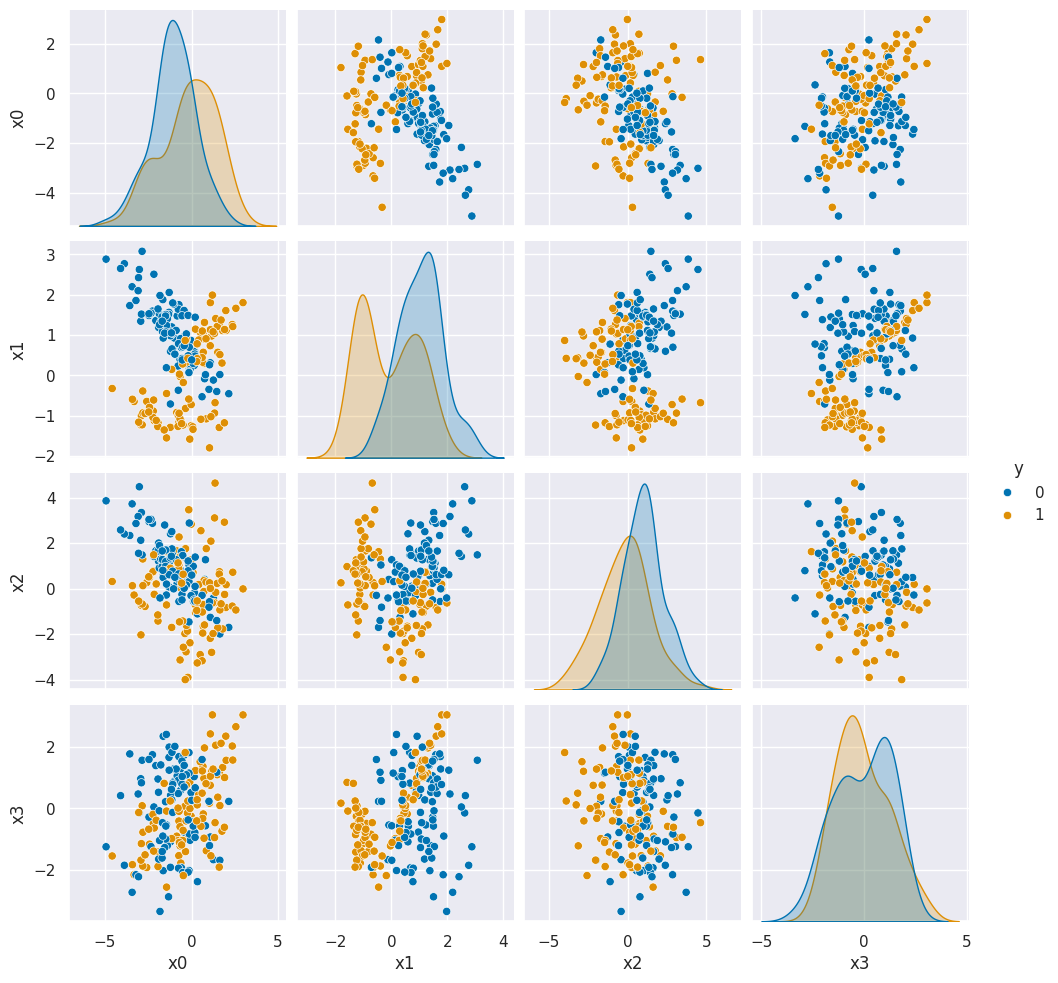
we can do it again with our template function by defining two functions: one for the hidden neuron and one for output, then the prediction
hidden_neuron_4d = lambda x: aritificial_neuron_template(identity_activation,
clf_4d.coefs_[0],clf_4d.intercepts_[0],x)
output_neuron_4d = lambda x: aritificial_neuron_template(logistic_activation,
clf_4d.coefs_[1],clf_4d.intercepts_[1],x)
output_neuron_4d(hidden_neuron_4d(pt_4d))
array([[0.95358788],
[0.85324909]])
clf_4d.predict_proba(pt_4d)
array([[0.04641212, 0.95358788],
[0.14675091, 0.85324909]])
and confirm it’s correct.
pt_4d_2 =np.asarray([[-.5,-2,-1,-1],[1.5,0,-.5,1]])
output_neuron_4d(hidden_neuron_4d(pt_4d_2))
array([[0.99145594],
[0.90639784]])
clf_4d.predict_proba(pt_4d_2)
array([[0.00854406, 0.99145594],
[0.09360216, 0.90639784]])
We can build up what we need for a 4 hidden neuron MLP too. First we’ll train the MLP
clf_4d_4h = MLPClassifier(
hidden_layer_sizes=(4),
max_iter=500,
alpha=1e-4,
solver="lbfgs",
verbose=10,
activation='logistic'
)
clf_4d_4h.fit(X_train, y_train)
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 25 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 6.86993D-01 |proj g|= 5.15503D-02
At iterate 1 f= 6.71843D-01 |proj g|= 4.81291D-02
At iterate 2 f= 6.11201D-01 |proj g|= 4.38953D-02
At iterate 3 f= 5.40478D-01 |proj g|= 5.29556D-02
At iterate 4 f= 4.96079D-01 |proj g|= 6.22516D-02
At iterate 5 f= 4.69397D-01 |proj g|= 3.20348D-02
At iterate 6 f= 4.47412D-01 |proj g|= 5.25604D-02
At iterate 7 f= 4.25078D-01 |proj g|= 1.81292D-02
At iterate 8 f= 4.14300D-01 |proj g|= 2.21372D-02
At iterate 9 f= 3.13232D-01 |proj g|= 5.29668D-02
At iterate 10 f= 2.55893D-01 |proj g|= 4.88671D-02
At iterate 11 f= 2.01154D-01 |proj g|= 5.60794D-02
At iterate 12 f= 1.86222D-01 |proj g|= 2.29334D-02
At iterate 13 f= 1.78364D-01 |proj g|= 1.70823D-02
At iterate 14 f= 1.56030D-01 |proj g|= 1.22533D-02
At iterate 15 f= 1.38981D-01 |proj g|= 1.06683D-02
At iterate 16 f= 1.28551D-01 |proj g|= 8.28843D-03
At iterate 17 f= 1.22909D-01 |proj g|= 1.02772D-02
At iterate 18 f= 1.19455D-01 |proj g|= 5.37004D-03
At iterate 19 f= 1.14854D-01 |proj g|= 2.63923D-03
At iterate 20 f= 1.12021D-01 |proj g|= 5.46547D-03
At iterate 21 f= 1.08211D-01 |proj g|= 9.03422D-03
At iterate 22 f= 1.02509D-01 |proj g|= 8.47140D-03
At iterate 23 f= 9.82937D-02 |proj g|= 5.87285D-03
At iterate 24 f= 9.40374D-02 |proj g|= 2.77348D-03
At iterate 25 f= 9.25076D-02 |proj g|= 2.91121D-03
At iterate 26 f= 8.98174D-02 |proj g|= 7.12924D-03
At iterate 27 f= 8.82365D-02 |proj g|= 3.38542D-03
At iterate 28 f= 8.68338D-02 |proj g|= 2.37871D-03
At iterate 29 f= 8.48995D-02 |proj g|= 4.22036D-03
At iterate 30 f= 8.42852D-02 |proj g|= 5.21892D-03
At iterate 31 f= 8.31786D-02 |proj g|= 6.55434D-03
At iterate 32 f= 8.06873D-02 |proj g|= 1.16838D-02
At iterate 33 f= 7.61894D-02 |proj g|= 7.89277D-03
At iterate 34 f= 7.21708D-02 |proj g|= 2.28003D-02
At iterate 35 f= 7.02870D-02 |proj g|= 5.65231D-03
At iterate 36 f= 6.91244D-02 |proj g|= 5.01037D-03
At iterate 37 f= 6.68795D-02 |proj g|= 3.15619D-03
At iterate 38 f= 6.55812D-02 |proj g|= 7.81240D-03
At iterate 39 f= 6.35301D-02 |proj g|= 7.53858D-03
At iterate 40 f= 6.14805D-02 |proj g|= 1.05793D-02
At iterate 41 f= 5.80625D-02 |proj g|= 2.07321D-03
At iterate 42 f= 5.75816D-02 |proj g|= 1.08850D-03
At iterate 43 f= 5.69555D-02 |proj g|= 8.84371D-04
At iterate 44 f= 5.66800D-02 |proj g|= 6.40567D-04
At iterate 45 f= 5.65004D-02 |proj g|= 7.28330D-04
At iterate 46 f= 5.63871D-02 |proj g|= 5.62131D-04
At iterate 47 f= 5.63435D-02 |proj g|= 9.96171D-04
At iterate 48 f= 5.62820D-02 |proj g|= 4.88708D-04
At iterate 49 f= 5.62423D-02 |proj g|= 4.04656D-04
At iterate 50 f= 5.61874D-02 |proj g|= 3.80582D-04
At iterate 51 f= 5.61425D-02 |proj g|= 3.05703D-04
At iterate 52 f= 5.61022D-02 |proj g|= 2.04803D-04
At iterate 53 f= 5.60590D-02 |proj g|= 6.19325D-04
At iterate 54 f= 5.59989D-02 |proj g|= 3.51337D-04
At iterate 55 f= 5.58804D-02 |proj g|= 3.00464D-04
At iterate 56 f= 5.57899D-02 |proj g|= 5.29091D-04
At iterate 57 f= 5.56706D-02 |proj g|= 6.46040D-04
At iterate 58 f= 5.56216D-02 |proj g|= 1.36581D-03
At iterate 59 f= 5.55088D-02 |proj g|= 2.60926D-04
At iterate 60 f= 5.54751D-02 |proj g|= 2.01477D-04
At iterate 61 f= 5.54198D-02 |proj g|= 4.32818D-04
At iterate 62 f= 5.53570D-02 |proj g|= 3.67092D-04
At iterate 63 f= 5.52725D-02 |proj g|= 3.64889D-04
At iterate 64 f= 5.52607D-02 |proj g|= 4.42936D-04
At iterate 65 f= 5.52043D-02 |proj g|= 3.53198D-04
At iterate 66 f= 5.51655D-02 |proj g|= 4.64748D-04
At iterate 67 f= 5.51210D-02 |proj g|= 1.78778D-04
At iterate 68 f= 5.50443D-02 |proj g|= 2.36651D-04
At iterate 69 f= 5.49911D-02 |proj g|= 3.03305D-04
At iterate 70 f= 5.49714D-02 |proj g|= 1.97655D-04
At iterate 71 f= 5.49425D-02 |proj g|= 1.03619D-04
At iterate 72 f= 5.49227D-02 |proj g|= 7.89413D-05
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
25 72 83 1 0 0 7.894D-05 5.492D-02
F = 5.4922664996025897E-002
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
This problem is unconstrained.
MLPClassifier(activation='logistic', hidden_layer_sizes=4, max_iter=500,
solver='lbfgs', verbose=10)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
MLPClassifier(activation='logistic', hidden_layer_sizes=4, max_iter=500,
solver='lbfgs', verbose=10)Then use our function to build up the predictions
hidden_neuron_4d_h0 = lambda x: aritificial_neuron_template(logistic_activation,
clf_4d_4h.coefs_[0][:,0],clf_4d_4h.intercepts_[0][0],x)
hidden_neuron_4d_h1 = lambda x: aritificial_neuron_template(logistic_activation,
clf_4d_4h.coefs_[0][:,1],clf_4d_4h.intercepts_[0][1],x)
hidden_neuron_4d_h2 = lambda x: aritificial_neuron_template(logistic_activation,
clf_4d_4h.coefs_[0][:,2],clf_4d_4h.intercepts_[0][2],x)
hidden_neuron_4d_h3 = lambda x: aritificial_neuron_template(logistic_activation,
clf_4d_4h.coefs_[0][:,3],clf_4d_4h.intercepts_[0][3],x)
output_neuron_4d_4h = lambda x: aritificial_neuron_template(logistic_activation,
clf_4d_4h.coefs_[1],clf_4d_4h.intercepts_[1],x)
and finally call it all togther
output_neuron_4d_4h(np.asarray([hidden_neuron_4d_h0(pt_4d),
hidden_neuron_4d_h1(pt_4d),
hidden_neuron_4d_h2(pt_4d),
hidden_neuron_4d_h3(pt_4d)]).T)
array([[0.99946891],
[0.928926 ]])
and compare with the MLP’s own predications
clf_4d_4h.predict_proba(pt_4d)
array([[5.31087115e-04, 9.99468913e-01],
[7.10740021e-02, 9.28925998e-01]])
23.8. Questions#
23.8.1. Are there neural networks wherein each layer does a different type of transformation, such as logistic or identity?#
There are different types of layers and some are defined by activations, others are more complex calculations in other ways.
23.8.2. What are the benefits of neural networks compared to machine learning?#
Neural networks are one type of machine learning model.
23.8.3. What is the larger contributing in advancements in deep learning - hardware or software?#
Hardware advances were essential for
23.8.4. Are there any other visualizations of neural networks such as images,articles,videos that would be good for introductions? I would like some that do go into some of the math behind how it works.#
This free textbook is a good source by leaders in the feild.
23.8.5. Are you able to keep training data from a previous session with deep learning?#
For any machine learning algorithm you can save the object or serialize the parameters to a file and then load them back in.
For deep learning you can save the weight matrices and you can also then reinstantiate the object.
Hugging face contains pretrained models.
23.8.6. What other functions can we use instead of explit (sigmoid)?#
The most common other one is RELU, we’ll see more about that next week.
