Class 29: Choosing a Model¶
log onto prismia
share your favorite restaraunt on/near campus in the zoom chat
Portfolio PR¶
# %load http://drsmb.co/310
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import pandas as pd
from sklearn import datasets
from sklearn import cluster
from sklearn import svm
from sklearn import tree
from sklearn import model_selection
iris_X, iris_y = datasets.load_iris(return_X_y= True)
iris_X_train, iris_X_test, iris_y_train, iris_y_test = model_selection.train_test_split(iris_X,iris_y)
dt = tree.DecisionTreeClassifier()
params_dt = {'criterion':['gini','entropy'],'max_depth':[2,3,4],
'min_samples_leaf':list(range(2,20,2))}
dt_opt = model_selection.GridSearchCV(dt,params_dt)
dt_opt.fit(iris_X_train,iris_y_train)
GridSearchCV(estimator=DecisionTreeClassifier(),
param_grid={'criterion': ['gini', 'entropy'],
'max_depth': [2, 3, 4],
'min_samples_leaf': [2, 4, 6, 8, 10, 12, 14, 16, 18]})
dt_opt.predict(iris_X_test)
array([1, 0, 0, 1, 2, 2, 0, 2, 0, 2, 0, 0, 2, 1, 2, 0, 2, 2, 2, 2, 0, 2,
2, 0, 2, 1, 0, 1, 1, 0, 0, 2, 1, 2, 2, 1, 2, 2])
dt_opt.best_estimator_.predict(iris_X_test)
array([1, 0, 0, 1, 2, 2, 0, 2, 0, 2, 0, 0, 2, 1, 2, 0, 2, 2, 2, 2, 0, 2,
2, 0, 2, 1, 0, 1, 1, 0, 0, 2, 1, 2, 2, 1, 2, 2])
pd.DataFrame(dt_opt.cv_results_)
| mean_fit_time | std_fit_time | mean_score_time | std_score_time | param_criterion | param_max_depth | param_min_samples_leaf | params | split0_test_score | split1_test_score | split2_test_score | split3_test_score | split4_test_score | mean_test_score | std_test_score | rank_test_score | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.000561 | 0.000138 | 0.000276 | 0.000041 | gini | 2 | 2 | {'criterion': 'gini', 'max_depth': 2, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 1 | 0.000443 | 0.000023 | 0.000238 | 0.000013 | gini | 2 | 4 | {'criterion': 'gini', 'max_depth': 2, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 2 | 0.000484 | 0.000022 | 0.000266 | 0.000011 | gini | 2 | 6 | {'criterion': 'gini', 'max_depth': 2, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 3 | 0.000447 | 0.000027 | 0.000239 | 0.000015 | gini | 2 | 8 | {'criterion': 'gini', 'max_depth': 2, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 4 | 0.000489 | 0.000022 | 0.000255 | 0.000008 | gini | 2 | 10 | {'criterion': 'gini', 'max_depth': 2, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 5 | 0.000473 | 0.000031 | 0.000244 | 0.000019 | gini | 2 | 12 | {'criterion': 'gini', 'max_depth': 2, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 6 | 0.000460 | 0.000031 | 0.000250 | 0.000013 | gini | 2 | 14 | {'criterion': 'gini', 'max_depth': 2, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 7 | 0.000447 | 0.000031 | 0.000249 | 0.000019 | gini | 2 | 16 | {'criterion': 'gini', 'max_depth': 2, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 8 | 0.000477 | 0.000021 | 0.000266 | 0.000032 | gini | 2 | 18 | {'criterion': 'gini', 'max_depth': 2, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 9 | 0.000475 | 0.000038 | 0.000248 | 0.000021 | gini | 3 | 2 | {'criterion': 'gini', 'max_depth': 3, 'min_sam... | 0.869565 | 0.913043 | 1.000000 | 1.000000 | 0.954545 | 0.947431 | 0.050642 | 1 |
| 10 | 0.000502 | 0.000014 | 0.000261 | 0.000023 | gini | 3 | 4 | {'criterion': 'gini', 'max_depth': 3, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 11 | 0.000470 | 0.000040 | 0.000243 | 0.000024 | gini | 3 | 6 | {'criterion': 'gini', 'max_depth': 3, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 12 | 0.000438 | 0.000026 | 0.000234 | 0.000016 | gini | 3 | 8 | {'criterion': 'gini', 'max_depth': 3, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 13 | 0.000474 | 0.000046 | 0.000252 | 0.000026 | gini | 3 | 10 | {'criterion': 'gini', 'max_depth': 3, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 14 | 0.000499 | 0.000018 | 0.000263 | 0.000010 | gini | 3 | 12 | {'criterion': 'gini', 'max_depth': 3, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 15 | 0.000500 | 0.000020 | 0.000258 | 0.000008 | gini | 3 | 14 | {'criterion': 'gini', 'max_depth': 3, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 16 | 0.000495 | 0.000023 | 0.000259 | 0.000009 | gini | 3 | 16 | {'criterion': 'gini', 'max_depth': 3, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 17 | 0.000481 | 0.000022 | 0.000249 | 0.000015 | gini | 3 | 18 | {'criterion': 'gini', 'max_depth': 3, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 18 | 0.000486 | 0.000025 | 0.000246 | 0.000021 | gini | 4 | 2 | {'criterion': 'gini', 'max_depth': 4, 'min_sam... | 0.869565 | 0.913043 | 1.000000 | 1.000000 | 0.954545 | 0.947431 | 0.050642 | 1 |
| 19 | 0.000499 | 0.000019 | 0.000257 | 0.000008 | gini | 4 | 4 | {'criterion': 'gini', 'max_depth': 4, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 20 | 0.000481 | 0.000033 | 0.000250 | 0.000025 | gini | 4 | 6 | {'criterion': 'gini', 'max_depth': 4, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 21 | 0.000476 | 0.000029 | 0.000251 | 0.000017 | gini | 4 | 8 | {'criterion': 'gini', 'max_depth': 4, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 22 | 0.000480 | 0.000043 | 0.000248 | 0.000020 | gini | 4 | 10 | {'criterion': 'gini', 'max_depth': 4, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 23 | 0.000473 | 0.000036 | 0.000247 | 0.000023 | gini | 4 | 12 | {'criterion': 'gini', 'max_depth': 4, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 24 | 0.000497 | 0.000020 | 0.000255 | 0.000016 | gini | 4 | 14 | {'criterion': 'gini', 'max_depth': 4, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 25 | 0.000425 | 0.000049 | 0.000234 | 0.000027 | gini | 4 | 16 | {'criterion': 'gini', 'max_depth': 4, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 26 | 0.000433 | 0.000034 | 0.000225 | 0.000008 | gini | 4 | 18 | {'criterion': 'gini', 'max_depth': 4, 'min_sam... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 27 | 0.000472 | 0.000049 | 0.000247 | 0.000022 | entropy | 2 | 2 | {'criterion': 'entropy', 'max_depth': 2, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 28 | 0.000465 | 0.000039 | 0.000248 | 0.000017 | entropy | 2 | 4 | {'criterion': 'entropy', 'max_depth': 2, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 29 | 0.000451 | 0.000057 | 0.000229 | 0.000030 | entropy | 2 | 6 | {'criterion': 'entropy', 'max_depth': 2, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 30 | 0.000438 | 0.000037 | 0.000226 | 0.000025 | entropy | 2 | 8 | {'criterion': 'entropy', 'max_depth': 2, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 31 | 0.000412 | 0.000060 | 0.000224 | 0.000040 | entropy | 2 | 10 | {'criterion': 'entropy', 'max_depth': 2, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 32 | 0.000480 | 0.000034 | 0.000240 | 0.000025 | entropy | 2 | 12 | {'criterion': 'entropy', 'max_depth': 2, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 33 | 0.000465 | 0.000035 | 0.000246 | 0.000023 | entropy | 2 | 14 | {'criterion': 'entropy', 'max_depth': 2, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 34 | 0.000470 | 0.000032 | 0.000236 | 0.000024 | entropy | 2 | 16 | {'criterion': 'entropy', 'max_depth': 2, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 35 | 0.000443 | 0.000062 | 0.000224 | 0.000025 | entropy | 2 | 18 | {'criterion': 'entropy', 'max_depth': 2, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 36 | 0.000450 | 0.000054 | 0.000237 | 0.000034 | entropy | 3 | 2 | {'criterion': 'entropy', 'max_depth': 3, 'min_... | 0.869565 | 0.913043 | 0.909091 | 1.000000 | 0.954545 | 0.929249 | 0.044445 | 4 |
| 37 | 0.000466 | 0.000049 | 0.000223 | 0.000029 | entropy | 3 | 4 | {'criterion': 'entropy', 'max_depth': 3, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 38 | 0.000419 | 0.000030 | 0.000211 | 0.000014 | entropy | 3 | 6 | {'criterion': 'entropy', 'max_depth': 3, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 39 | 0.000478 | 0.000057 | 0.000237 | 0.000036 | entropy | 3 | 8 | {'criterion': 'entropy', 'max_depth': 3, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 40 | 0.000463 | 0.000032 | 0.000237 | 0.000017 | entropy | 3 | 10 | {'criterion': 'entropy', 'max_depth': 3, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 41 | 0.000427 | 0.000049 | 0.000225 | 0.000033 | entropy | 3 | 12 | {'criterion': 'entropy', 'max_depth': 3, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 42 | 0.000453 | 0.000041 | 0.000223 | 0.000026 | entropy | 3 | 14 | {'criterion': 'entropy', 'max_depth': 3, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 43 | 0.000422 | 0.000049 | 0.000224 | 0.000032 | entropy | 3 | 16 | {'criterion': 'entropy', 'max_depth': 3, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 44 | 0.000393 | 0.000039 | 0.000203 | 0.000021 | entropy | 3 | 18 | {'criterion': 'entropy', 'max_depth': 3, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 45 | 0.000459 | 0.000069 | 0.000225 | 0.000041 | entropy | 4 | 2 | {'criterion': 'entropy', 'max_depth': 4, 'min_... | 0.869565 | 0.956522 | 0.954545 | 1.000000 | 0.954545 | 0.947036 | 0.042449 | 3 |
| 46 | 0.000407 | 0.000035 | 0.000200 | 0.000014 | entropy | 4 | 4 | {'criterion': 'entropy', 'max_depth': 4, 'min_... | 0.869565 | 0.956522 | 0.954545 | 0.909091 | 0.954545 | 0.928854 | 0.034616 | 5 |
| 47 | 0.000489 | 0.000054 | 0.000256 | 0.000019 | entropy | 4 | 6 | {'criterion': 'entropy', 'max_depth': 4, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 48 | 0.000438 | 0.000053 | 0.000226 | 0.000027 | entropy | 4 | 8 | {'criterion': 'entropy', 'max_depth': 4, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 49 | 0.000413 | 0.000072 | 0.000209 | 0.000032 | entropy | 4 | 10 | {'criterion': 'entropy', 'max_depth': 4, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 50 | 0.000400 | 0.000035 | 0.000218 | 0.000026 | entropy | 4 | 12 | {'criterion': 'entropy', 'max_depth': 4, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 51 | 0.000445 | 0.000060 | 0.000241 | 0.000029 | entropy | 4 | 14 | {'criterion': 'entropy', 'max_depth': 4, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 52 | 0.000440 | 0.000031 | 0.000230 | 0.000024 | entropy | 4 | 16 | {'criterion': 'entropy', 'max_depth': 4, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
| 53 | 0.000470 | 0.000039 | 0.000255 | 0.000019 | entropy | 4 | 18 | {'criterion': 'entropy', 'max_depth': 4, 'min_... | 0.869565 | 0.913043 | 0.909091 | 0.909091 | 0.954545 | 0.911067 | 0.026924 | 6 |
df = pd.DataFrame(dt_opt.cv_results_)
df.plot('mean_score_time','mean_test_score')
<AxesSubplot:xlabel='mean_score_time'>
%load http://drsmb.co
param_grid = {'kernel':['linear','rbf'], 'C':[.5, 1, 10]}
svm_clf = svm.SVC(kernel='linear')
svm_opt =model_selection.GridSearchCV(svm_clf,param_grid,)
svm_opt.fit(iris_X_train, iris_y_train)
GridSearchCV(estimator=SVC(kernel='linear'),
param_grid={'C': [0.5, 1, 10], 'kernel': ['linear', 'rbf']})
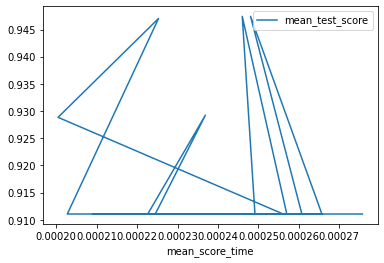
df_svm = pd.DataFrame(svm_opt.cv_results_)
df_svm.plot.scatter('mean_score_time','mean_test_score')
<AxesSubplot:xlabel='mean_score_time', ylabel='mean_test_score'>
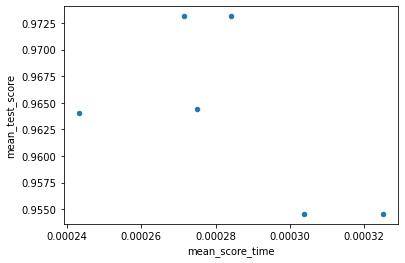
df_svm.plot.scatter('mean_score_time','std_test_score')
<AxesSubplot:xlabel='mean_score_time', ylabel='std_test_score'>