Contents

Class 31: Confidence Intervals

  1. respond in zoom chat: iced vs. hot coffee (or tea, or beverages in general). one all year? seasonal?

  2. log onto prismia chat

  3. respond on prismia with any questions you have about the course material so far:

  • what are you confused about?

  • wht do you want to know about about?

  • what thing keeps tripping you up on assignments?

Admin

Confidence intervals

# %load http://drsmb.co/310
# %load http://drsmb.co/310
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import pandas as pd
from sklearn import datasets
from sklearn import cluster
from sklearn import svm
from sklearn import tree
from sklearn import model_selection

iris_X , iris_y = datasets.load_iris(return_X_y= True)
iris_X_train, iris_X_test, iris_y_train, iris_y_test = model_selection.train_test_split(
            iris_X , iris_y,test_size =.2, random_state=0)

param_grid = {'kernel':['linear','rbf'], 'C':[.5, 1, 10]}
svm_clf = svm.SVC(kernel='linear')
svm_opt =model_selection.GridSearchCV(svm_clf,param_grid,)
svm_opt.fit(iris_X_train, iris_y_train)

df_svm = pd.DataFrame(svm_opt.cv_results_)
df_svm.sort_values(by='mean_score_time',inplace=True)
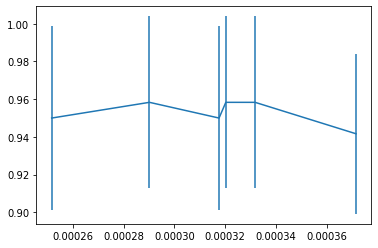
plt.errorbar(df_svm['mean_score_time'],df_svm['mean_test_score'], df_svm['std_test_score'])

<ErrorbarContainer object of 3 artists>
../_images/2020-11-20_4_1.png 
iris_X.shape

(150, 4)

training

150*.8

120.0

iris_X_train.shape

(120, 4)

Cross validation tests

120*.2

24.0

iris_X_test

array([[5.8, 2.8, 5.1, 2.4],
       [6. , 2.2, 4. , 1. ],
       [5.5, 4.2, 1.4, 0.2],
       [7.3, 2.9, 6.3, 1.8],
       [5. , 3.4, 1.5, 0.2],
       [6.3, 3.3, 6. , 2.5],
       [5. , 3.5, 1.3, 0.3],
       [6.7, 3.1, 4.7, 1.5],
       [6.8, 2.8, 4.8, 1.4],
       [6.1, 2.8, 4. , 1.3],
       [6.1, 2.6, 5.6, 1.4],
       [6.4, 3.2, 4.5, 1.5],
       [6.1, 2.8, 4.7, 1.2],
       [6.5, 2.8, 4.6, 1.5],
       [6.1, 2.9, 4.7, 1.4],
       [4.9, 3.6, 1.4, 0.1],
       [6. , 2.9, 4.5, 1.5],
       [5.5, 2.6, 4.4, 1.2],
       [4.8, 3. , 1.4, 0.3],
       [5.4, 3.9, 1.3, 0.4],
       [5.6, 2.8, 4.9, 2. ],
       [5.6, 3. , 4.5, 1.5],
       [4.8, 3.4, 1.9, 0.2],
       [4.4, 2.9, 1.4, 0.2],
       [6.2, 2.8, 4.8, 1.8],
       [4.6, 3.6, 1. , 0.2],
       [5.1, 3.8, 1.9, 0.4],
       [6.2, 2.9, 4.3, 1.3],
       [5. , 2.3, 3.3, 1. ],
       [5. , 3.4, 1.6, 0.4]])

svm_opt.score(iris_X_test,iris_y_test)

1.0

# %load http://drsmb.co/310
def classification_confint(acc, n):
    '''
    Compute the 95% confidence interval for a classification problem.
      acc -- classification accuracy
      n   -- number of observations used to compute the accuracy
    Returns a tuple (lb,ub)
    '''
    interval = 1.96*np.sqrt(acc*(1-acc)/n)
    lb = max(0, acc - interval)
    ub = min(1.0, acc + interval)
    return (lb,ub)

classification_confint(svm_opt.score(iris_X_test,iris_y_test),len(iris_y_test))

(1.0, 1.0)

classification_confint(.9999,len(iris_y_test))

(0.9963217248848085, 1.0)

classification_confint(.85,len(iris_y_test))

(0.722223632858028, 0.9777763671419719)

classification_confint(.93,len(iris_y_test))

(0.8386968127609995, 1.0)

classification_confint(.85,50)

(0.7510248516040516, 0.9489751483959483)

classification_confint(.93,50)

(0.8592768552735387, 1.0)

df_svm
mean_fit_time std_fit_time mean_score_time std_score_time param_C param_kernel params split0_test_score split1_test_score split2_test_score split3_test_score split4_test_score mean_test_score std_test_score rank_test_score
5 0.000566 0.000049 0.000252 0.000019 10 rbf {'C': 10, 'kernel': 'rbf'} 0.958333 0.916667 1.000000 1.0 0.875 0.950000 0.048591 4
4 0.000640 0.000034 0.000290 0.000014 10 linear {'C': 10, 'kernel': 'linear'} 0.958333 0.958333 1.000000 1.0 0.875 0.958333 0.045644 1
2 0.000668 0.000023 0.000318 0.000018 1 linear {'C': 1, 'kernel': 'linear'} 0.958333 0.916667 1.000000 1.0 0.875 0.950000 0.048591 4
0 0.000746 0.000053 0.000320 0.000031 0.5 linear {'C': 0.5, 'kernel': 'linear'} 0.958333 0.958333 1.000000 1.0 0.875 0.958333 0.045644 1
3 0.000738 0.000040 0.000332 0.000022 1 rbf {'C': 1, 'kernel': 'rbf'} 0.958333 0.958333 1.000000 1.0 0.875 0.958333 0.045644 1
1 0.000827 0.000016 0.000372 0.000015 0.5 rbf {'C': 0.5, 'kernel': 'rbf'} 0.916667 0.958333 0.958333 1.0 0.875 0.941667 0.042492 6

Try it yourself

How many samples would it take for accuracies of 85% and 93% to be statistically significantly different for 95% confidence interval?

the result is a tuple, so we can use indexing to select one element

then compare the upper bound for the lower accuracy to the lower bound of the upper to see if there’s overlap

Then we can make that a lambda and use a while loop to find the answer.

Class 30: Learning Curves, Validation Curves Class 32: Intro to NLP