17. Making Predictions in Generative Model#

import pandas as pd
import seaborn as sns
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import confusion_matrix, classification_report, roc_auc_score
iris_df = sns.load_dataset('iris')

We’ll load the data again

iris_df.head(1)

	sepal_length	sepal_width	petal_length	petal_width	species
0	5.1	3.5	1.4	0.2	setosa

Next we indicate the feature variables and target and split into test and train sets. Well use 80% of the data for training.

feature_vars = ['sepal_length', 'sepal_width','petal_length', 'petal_width',]
target_var = 'species'

X_train, X_test, y_train, y_test = train_test_split(iris_df[feature_vars],
                          iris_df[target_var], train_size=.8, random_state=0)

We can confirm the shape is as expected

X_train.shape

(120, 4)

iris_df.shape

(150, 5)

.8*150

120.0

Next we again initialize and fit the classifier

gnb = GaussianNB()
gnb.fit(X_train, y_train)

GaussianNB()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

We can compute predictions

y_pred = gnb.predict(X_test)
y_pred

array(['virginica', 'versicolor', 'setosa', 'virginica', 'setosa',
       'virginica', 'setosa', 'versicolor', 'versicolor', 'versicolor',
       'versicolor', 'versicolor', 'versicolor', 'versicolor',
       'versicolor', 'setosa', 'versicolor', 'versicolor', 'setosa',
       'setosa', 'virginica', 'versicolor', 'setosa', 'setosa',
       'virginica', 'setosa', 'setosa', 'versicolor', 'versicolor',
       'setosa'], dtype='<U10')

And score the results

gnb.score(X_test,y_test)

0.9666666666666667

We saw last week that when we fit the Gaussian Naive Bayes, it computes a mean \(\theta\) and variance \(\sigma\) and adds them to model parameters in attributes gnb.theta_, gnb.sigma_.

When we use the predict method, it uses those parameters to calculate the likelihood of the sample according to a Gaussian distribution (normal) for each class and then calculates the probability of the sample belonging to each class.

gnb.predict_proba(X_test)

array([[1.63380783e-232, 2.18878438e-006, 9.99997811e-001],
       [1.82640391e-082, 9.99998304e-001, 1.69618390e-006],
       [1.00000000e+000, 7.10250510e-019, 3.65449801e-028],
       [1.58508262e-305, 1.04649020e-006, 9.99998954e-001],
       [1.00000000e+000, 8.59168655e-017, 4.22159374e-027],
       [6.39815011e-321, 1.56450314e-010, 1.00000000e+000],
       [1.00000000e+000, 1.09797313e-016, 5.30276557e-027],
       [1.25122812e-146, 7.74052109e-001, 2.25947891e-001],
       [5.34357526e-150, 9.07564955e-001, 9.24350453e-002],
       [5.67261712e-093, 9.99882109e-001, 1.17891111e-004],
       [2.38651144e-210, 5.29609631e-001, 4.70390369e-001],
       [8.12047631e-132, 9.43762575e-001, 5.62374248e-002],
       [5.25177109e-132, 9.98864361e-001, 1.13563851e-003],
       [1.24498038e-139, 9.49838641e-001, 5.01613586e-002],
       [4.08232760e-140, 9.88043864e-001, 1.19561365e-002],
       [1.00000000e+000, 7.12837229e-019, 4.10162749e-029],
       [4.19553996e-131, 9.87944980e-001, 1.20550201e-002],
       [4.13286716e-111, 9.99942383e-001, 5.76167389e-005],
       [1.00000000e+000, 2.24933112e-015, 3.63624519e-026],
       [1.00000000e+000, 9.86750131e-016, 2.42355087e-025],
       [1.85930865e-186, 1.66966805e-002, 9.83303319e-001],
       [8.83060167e-130, 9.92757232e-001, 7.24276827e-003],
       [1.00000000e+000, 4.26380344e-013, 4.34222344e-023],
       [1.00000000e+000, 1.28045851e-016, 1.26708019e-027],
       [2.43739221e-168, 1.83516225e-001, 8.16483775e-001],
       [1.00000000e+000, 2.62431469e-018, 6.72573168e-029],
       [1.00000000e+000, 3.20605389e-011, 1.52433420e-020],
       [2.20964201e-110, 9.99291229e-001, 7.08771072e-004],
       [1.39297338e-046, 9.99999972e-001, 2.81392389e-008],
       [1.00000000e+000, 1.85943966e-013, 1.58833385e-023]])

These are hard to interpret as is, one option is to plot them

# make the prbabilities into a dataframe labeled with classes & make the index a separate column
prob_df = pd.DataFrame(data = gnb.predict_proba(X_test), columns = gnb.classes_ ).reset_index()
# add the predictions
prob_df['predicted_species'] = y_pred
prob_df['true_species'] = y_test.values
# for plotting, make a column that combines the index & prediction
pred_text = lambda r: str( r['index']) + ',' + r['predicted_species']
prob_df['i,pred'] = prob_df.apply(pred_text,axis=1)
# same for ground truth
true_text = lambda r: str( r['index']) + ',' + r['true_species']
prob_df['correct'] = prob_df['predicted_species'] == prob_df['true_species']
# a dd a column for which are correct
prob_df['i,true'] = prob_df.apply(true_text,axis=1)
prob_df_melted = prob_df.melt(id_vars =[ 'index', 'predicted_species','true_species','i,pred','i,true','correct'],value_vars = gnb.classes_,
                             var_name = target_var, value_name = 'probability')
prob_df_melted.head()

	index	predicted_species	true_species	i,pred	i,true	correct	species	probability
0	0	virginica	virginica	0,virginica	0,virginica	True	setosa	1.633808e-232
1	1	versicolor	versicolor	1,versicolor	1,versicolor	True	setosa	1.826404e-82
2	2	setosa	setosa	2,setosa	2,setosa	True	setosa	1.000000e+00
3	3	virginica	virginica	3,virginica	3,virginica	True	setosa	1.585083e-305
4	4	setosa	setosa	4,setosa	4,setosa	True	setosa	1.000000e+00

Now we have a data frame where each rown is one the probability of one sample belonging to one class. So there’s a total of number_of_samples*number_of_classes rows

prob_df_melted.shape

(90, 8)

len(y_pred)*len(gnb.classes_)

One way to look at these is to, for each sample in the test set, make a bar chart of the probability it belongs to each class. We added to the data frame information so that we can plot this with the true class in the title using col = 'i,true'

sns.set_theme(font_scale=2, palette= "colorblind")
# plot a bar graph for each point labeled with the prediction
sns.catplot(data =prob_df_melted, x = 'species', y='probability' ,col ='i,true',
            col_wrap=5,kind='bar')

<seaborn.axisgrid.FacetGrid at 0x7fd4af264ca0>

We see that most sampples have nearly all of their probability mass (all probabiilties in a distribution sum (or integrate if continuous) to 1, but a few samples are not.

Try it yourself

Try adding a column that could change the headings to include an indicator of which are correct or not)

For now, we’ll group and look at on average, what the distributions are for correct vs incorrect based on predictions.

sns.set(font_scale=1.25, palette= "colorblind")
sns.catplot(data =prob_df_melted, x = 'species', y='probability' ,
            col ='predicted_species',row ='correct', kind='bar')

<seaborn.axisgrid.FacetGrid at 0x7fd4c038e9d0>

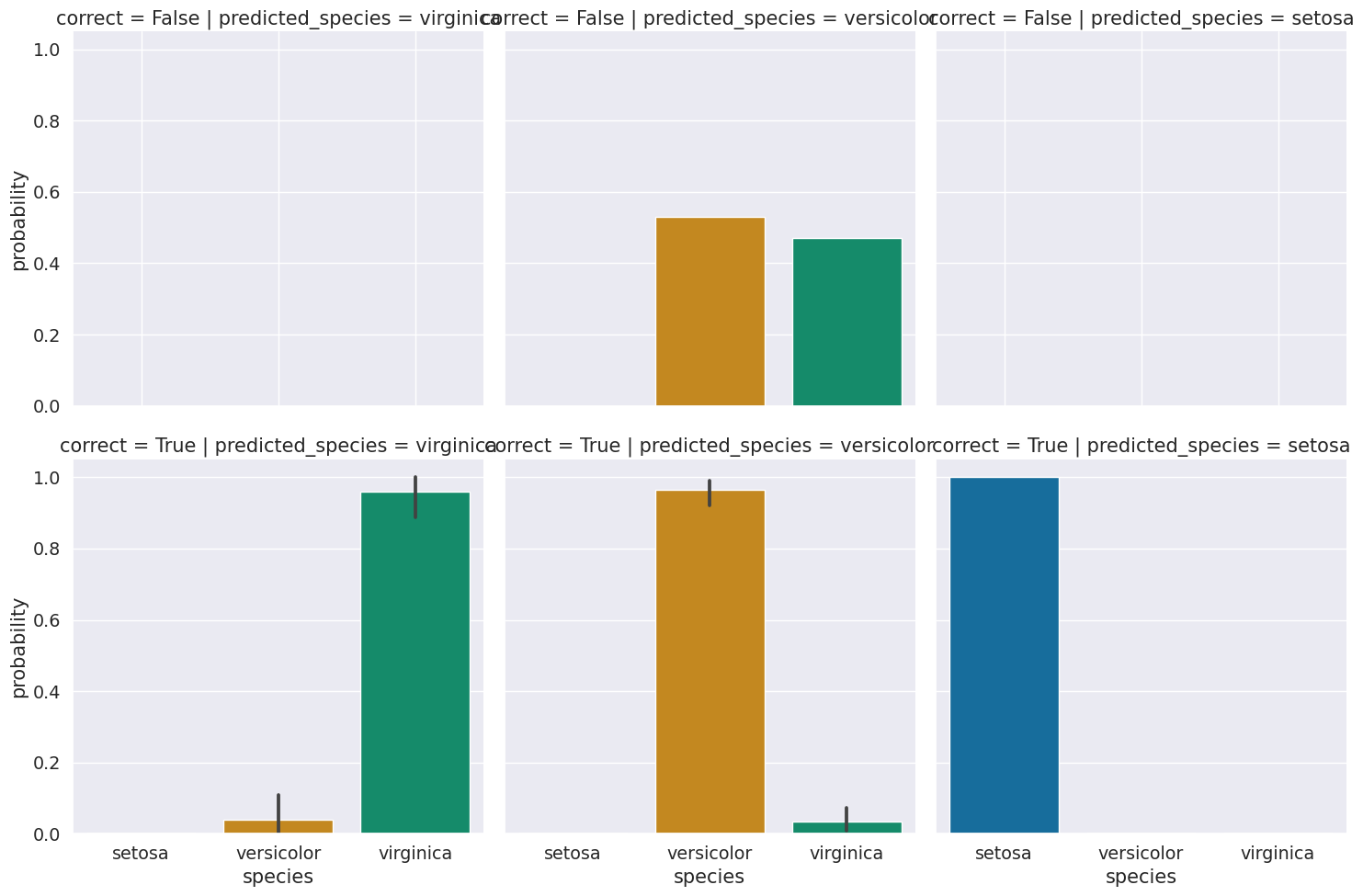
We see that the errors were all for versicolor, and on average the distribution is very uncertain for those samples. Those samples are probably hard to distinguish. We could check by creating a data frame with the data and the information about predictions and correct values.

prob_data_df = pd.concat([prob_df,X_test.reset_index()],axis=1).drop(columns=['index'])
prob_data_df.head(2)

	setosa	versicolor	virginica	predicted_species	true_species	i,pred	correct	i,true	sepal_length	sepal_width	petal_length	petal_width
0	1.633808e-232	0.000002	0.999998	virginica	virginica	0,virginica	True	0,virginica	5.8	2.8	5.1	2.4
1	1.826404e-82	0.999998	0.000002	versicolor	versicolor	1,versicolor	True	1,versicolor	6.0	2.2	4.0	1.0

feature_vars

['sepal_length', 'sepal_width', 'petal_length', 'petal_width']

g = sns.PairGrid(prob_data_df,x_vars=feature_vars,y_vars= feature_vars,hue='true_species')

g.map_diag(sns.kdeplot)
g.map_offdiag(sns.scatterplot, size=prob_data_df["correct"])

g.add_legend()

<seaborn.axisgrid.PairGrid at 0x7fd4ae680820>

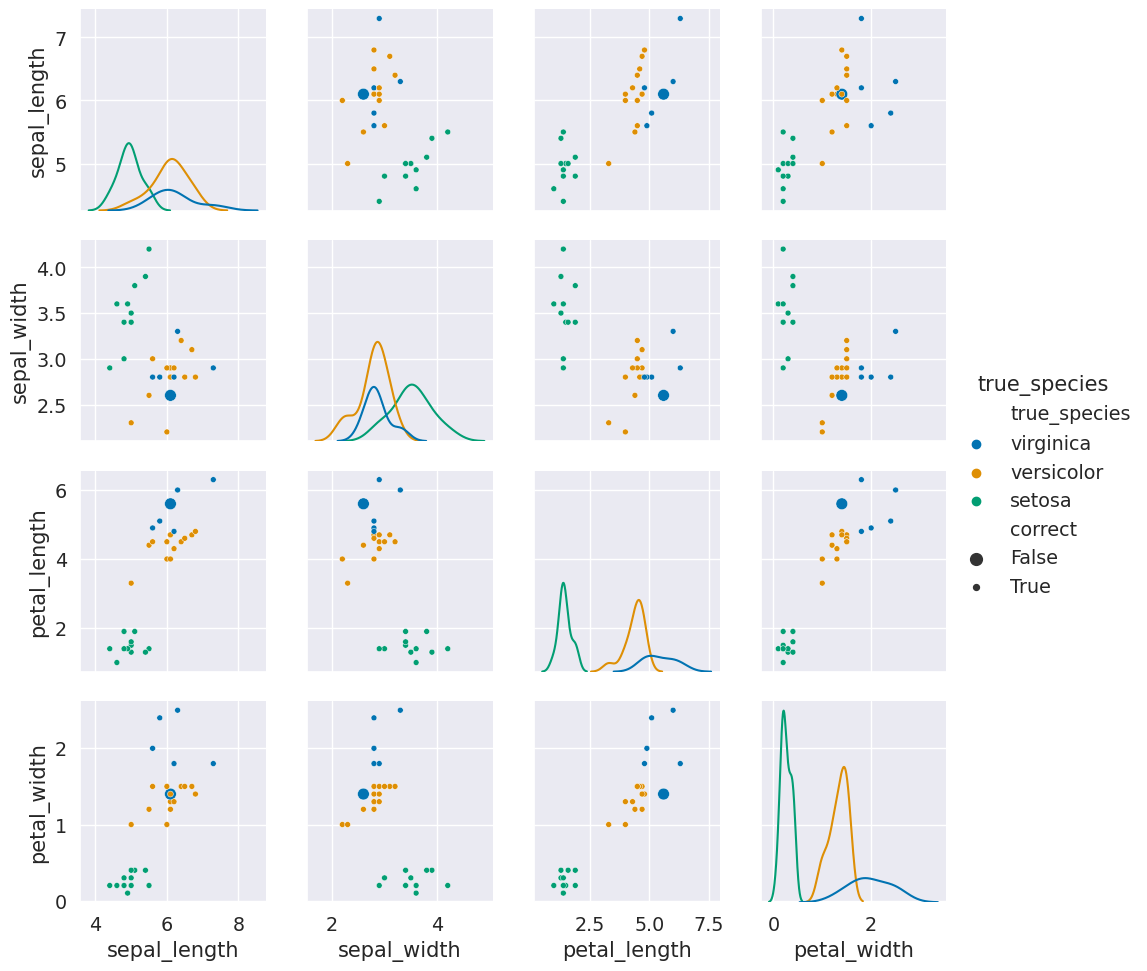
Here we see that the large dots (the incorrect ones) are all nearby to points of a different color. They were in fact samples that are similar to the other species. So again, this result makes sense and helps us see when classifiers that are a good fit for the data will still make mistakes.

We can also look at the probabilites of the predicted sample using max

p_predicted = np.max(gnb.predict_proba(X_test),axis=1)
p_predicted

array([0.99999781, 0.9999983 , 1.        , 0.99999895, 1.        ,
       1.        , 1.        , 0.77405211, 0.90756495, 0.99988211,
       0.52960963, 0.94376258, 0.99886436, 0.94983864, 0.98804386,
       1.        , 0.98794498, 0.99994238, 1.        , 1.        ,
       0.98330332, 0.99275723, 1.        , 1.        , 0.81648378,
       1.        , 1.        , 0.99929123, 0.99999997, 1.        ])

We see here that most of the predictions are pretty confident. We can also use the probabilities to then compute predictions and compare these to what the predict method gave, to confirm that this is how the predict method works.

pd.DataFrame(data = gnb.predict_proba(X_test), columns = gnb.classes_ ).idxmax(axis=1) ==y_pred

   True
   True
   True
   True
   True
   True
   True
   True
   True
   True
  True
  True
  True
  True
  True
  True
  True
  True
  True
  True
  True
  True
  True
  True
  True
  True
  True
  True
  True
  True
dtype: bool

Programming for Data Science at URI Fall 2021

Making Predictions in Generative Model

17. Making Predictions in Generative Model#