25. ML Task Review and Cross Validation

25.1. Relationship between Tasks

We learned classification first, because it shares similarities with each regression and clustering, while regression and clustering have less in common.

Classification is supervised learning for a categorical target.
Regression is supervised learning for a continuous target. Clustering is unsupervised learning for a categorical target.

Sklearn provides a nice flow chart for thinking through this.

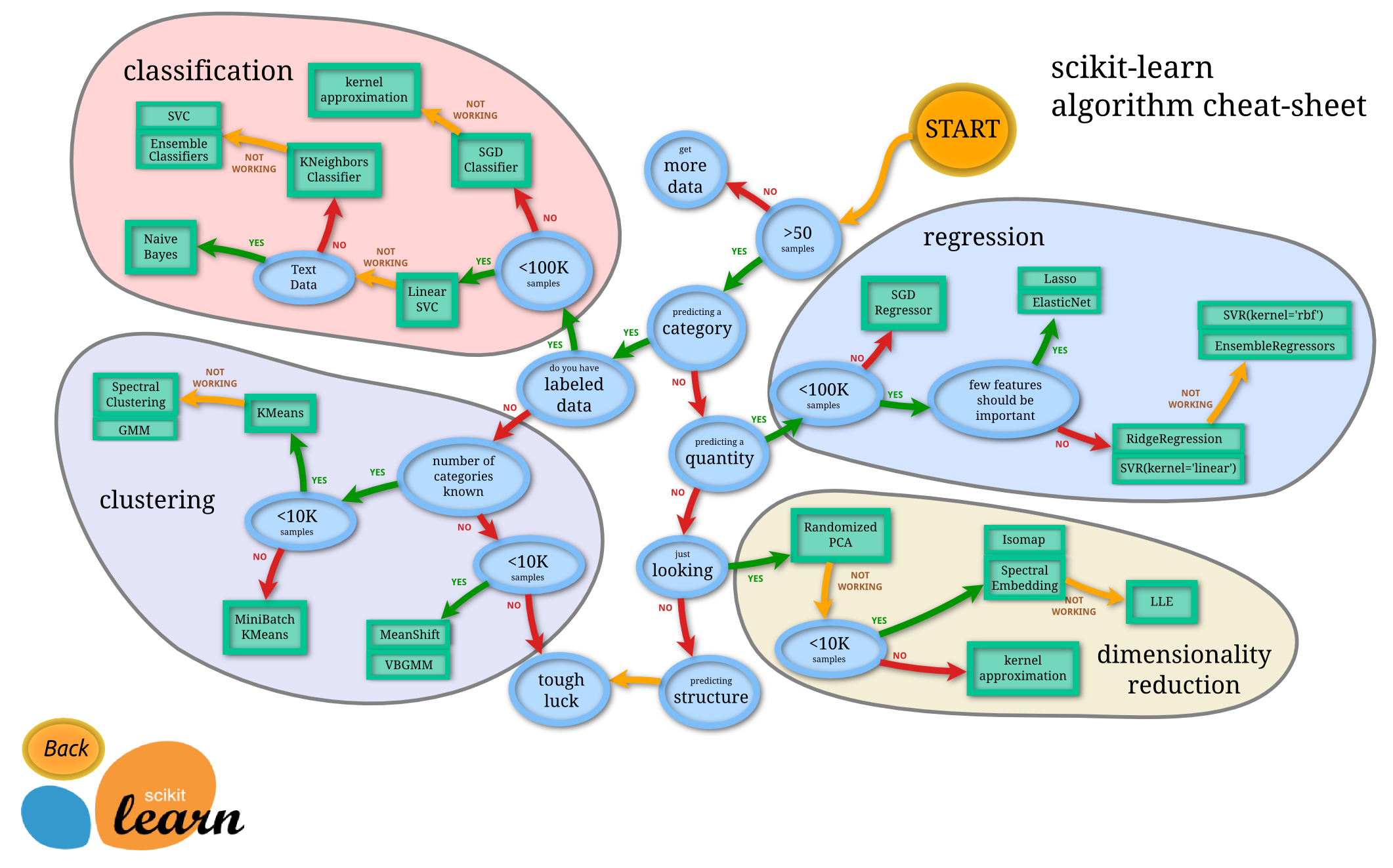
Predicting a category is another way of saying categorical target. Predicting a quantitiy is another way of saying continuous target. Having lables or not is the difference between

The flowchart assumes you know what you want to do with data and that is the ideal scenario. You have a dataset and you have a goal. For the purpose of getting to practice with a variety of things, in this course we ask you to start with a task and then find a dataset. Assignment 9 is the last time that’s true however. Starting with Assignment 10 and the last portflios, you can choose and focus on a specific application domain and then choose the right task from there.

Thinking about this, however, you use this information to move between the tasks within a given type of data. For example, you can use the same data for clustering as you did for classification. Switching the task changes the questions though: classification evaluation tells us how separable the classes are given that classifiers decision rule. Clustering can find other subgroups or the same ones, so the evaluation we choose allows us to explore this in more ways.

Regression requires a continuous target, so we need a dataset to be suitable for that, we can’t transform from the classification dataset to a regression one.
However, we can go the other way and that’s how some classification datasets are created.

The UCI adult Dataset is a popular ML dataset that was dervied from census data. The goal is to use a variety of features to predict if a person makes more than \(50k per year or not. While income is a continuous value, they applied a threshold (\)50k) to it to make a binary variable. The dataset does not include income in dollars, only the binary indicator.

Further Reading

Recent work reconsturcted the dataset with the continuous valued income. Their repository contains the data as well as links to their paper and a video of their talk on it.

25.2. Cross Validation

This week our goal is to learn how to optmize models. The first step in that is to get a good estimate of its performance.

We have seen that the test train splits, which are random, influence the performance.

import pandas as pd
import seaborn as sns
import numpy as np
from sklearn import tree
from sklearn.model_selection import cross_val_score
from sklearn.model_selection import train_test_split
from sklearn.cluster import KMeans
from sklearn import metrics

We’ll use the Iris data with a decision tree.

iris_df = sns.load_dataset('iris')

iris_X = iris_df.drop(columns=['species'])
iris_y = iris_df['species']

dt =tree.DecisionTreeClassifier()

We can split the data, fit the model, then compute a score, but since the splitting is a randomized step, the score is a random variable.

For example, if we have a coin that we want to see if it’s fair or not. We would flip it to test. One flip doesn’t tell us, but if we flip it a few times, we can estimate the probability it is heads by counting how many of the flips are heads and dividing by how many flips.

We can do something similar with our model performance. We can split the data a bunch of times and compute the score each time.

cross_val_score does this all for us.

It takes an estimator object and the data.

By default it uses 5-fold cross validation. It splits the data into 5 sections, then uses 4 of them to train and one to test. It then iterates through so that each section gets used for testing.

cross_val_score(dt,iris_X,iris_y,)

array([0.96666667, 0.96666667, 0.9       , 1.        , 1.        ])

We get back a score for each section or “fold” of the data. We can average those to get a single estimate.

np.mean(cross_val_score(dt,iris_X,iris_y,))

0.9533333333333334

We can use more folds.

cross_val_score(dt,iris_X,iris_y,cv=10)

array([1.        , 0.93333333, 1.        , 0.93333333, 0.93333333,
       0.86666667, 0.93333333, 0.93333333, 1.        , 1.        ])

Try it yourself

What is the equivalent train_size for 5 fold? what about 10-fold?

np.mean(cross_val_score(dt,iris_X,iris_y,cv=10))

0.96

We can use any estimator object here.

km = KMeans(n_clusters=3)

cross_val_score(km,iris_X,)

array([ -9.062     , -14.93195873, -18.93234207, -23.70894258,
       -19.55457726])

25.3. Notes

1. Assignments 9 assesses up to level 2 for classification

2. Heads up: Assignment 10 and 11 ask you to explore your work from 2 of (7,8,9) by optimizing the parameter and comparing different models for the same task. So the dataset selection problem is going away, little by little.