Predicting with Neural Networks
Contents
33. Predicting with Neural Networks#
from scipy.special import expit
from sklearn.datasets import make_classification
from sklearn.neural_network import MLPClassifier
from sklearn import svm
import pandas as pd
import numpy as np
import sklearn
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn import model_selection
# from skearn.model_selection import train_test_split
import seaborn as sns
sns.set_theme(palette='colorblind')
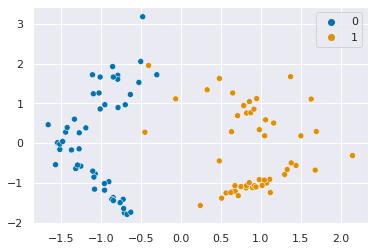
Today, were going to use very simple data in order to examin how a neural network works.
X, y = make_classification(n_samples=100, random_state=1,n_features=2,n_redundant=0)
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, stratify=y,
random_state=1)
sns.scatterplot(x=X[:,0],y=X[:,1],hue=y)
<AxesSubplot:>
First, we’ll train and score a tiny neural net: with 1 hidden layer of 1 neuron.
clf = MLPClassifier(
hidden_layer_sizes=(1), # 1 hidden layer, 1 aritficial neuron
max_iter=100, # maximum 100 interations in optimization
alpha=1e-4, # regularization
solver="lbfgs", #optimization algorithm
verbose=10, # how much detail to print
activation= 'identity' # how to transform the hidden layer beofore passing it to the next layer
)
clf.fit(X_train, y_train)
clf.score(X_test, y_test)
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 5 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 2.34381D+00 |proj g|= 1.10750D+00
At iterate 1 f= 1.15884D+00 |proj g|= 5.22275D-01
At iterate 2 f= 7.01374D-01 |proj g|= 9.09004D-02
At iterate 3 f= 6.76700D-01 |proj g|= 9.43005D-02
At iterate 4 f= 1.73953D-01 |proj g|= 3.30244D-01
At iterate 5 f= 5.13513D-02 |proj g|= 2.94368D-02
At iterate 6 f= 4.99313D-02 |proj g|= 1.89818D-02
At iterate 7 f= 4.87264D-02 |proj g|= 5.76625D-03
At iterate 8 f= 4.86119D-02 |proj g|= 4.00697D-03
At iterate 9 f= 4.84878D-02 |proj g|= 1.92688D-03
At iterate 10 f= 4.83939D-02 |proj g|= 1.64081D-03
At iterate 11 f= 4.82015D-02 |proj g|= 3.84407D-03
At iterate 12 f= 4.80076D-02 |proj g|= 3.82976D-03
At iterate 13 f= 4.79248D-02 |proj g|= 9.15466D-04
At iterate 14 f= 4.79198D-02 |proj g|= 2.37753D-04
At iterate 15 f= 4.79196D-02 |proj g|= 5.87358D-05
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
5 15 18 1 0 0 5.874D-05 4.792D-02
F = 4.7919620535136993E-002
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
This problem is unconstrained.
1.0
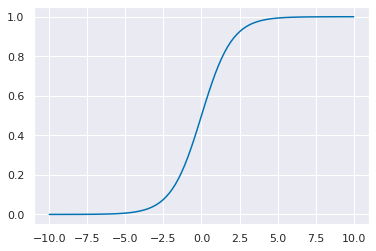
Now we can see that it actually has another activation, that we didn’t change the output layer still has a logistic activation layer, which we want. If we didn’t then the output layer wouldn’t be able to be interpretted as a probability, because probability always needs to be between 0 and 1.
clf.out_activation_
'logistic'
The logistic function looks like this:
x_logistic = np.linspace(-10,10,100)
y_logistic = expit(x_logistic)
plt.plot(x_logistic,y_logistic)
[<matplotlib.lines.Line2D at 0x7f49d5ab9760>]
The fit method learned the following weights:
clf.coefs_
[array([[-6.85186628],
[ 0.19720034]]),
array([[-1.91807161]])]
and biases
clf.intercepts_
[array([0.02652099]), array([5.74570119])]
These are called coefficients and intercepts because the weights are mutliplied by the inputs and the biases you can interpret as geometrically as shifting things, like a line intercept (recall y=mx+b)
33.1. Reconstructing the Predict method#
we’ll use an acutally new point, we can make one up
type([[-1,2]])
list
we want a numpy array so we will cast it
pt = np.array([[-1,2]])
type(pt)
numpy.ndarray
numpy’s matmul does matrix multiplicaion (multiply columns by rows element wise and sum)
the \(g\) is the activation function, which we set to identity \(g(x) = x\) so we don’t have to do more
np.matmul(pt,clf.coefs_[0]) + clf.intercepts_[0])*clf.coefs_[1] + clf.intercepts_[1])
Input In [11]
np.matmul(pt,clf.coefs_[0]) + clf.intercepts_[0])*clf.coefs_[1] + clf.intercepts_[1])
^
SyntaxError: unmatched ')'
but we’re not quite done, the output layer still transforms using the logistic
function, which is also known as expit and we have imported from scipy.
expit((np.matmul(pt,clf.coefs_[0]) + clf.intercepts_[0])*clf.coefs_[1] + clf.intercepts_[1])
array([[0.00027347]])
We can compare this to the classifier’s output. It outputs a probability for
each class, we only comptued the probabilyt of the 1 class.
clf.predict_proba(pt)
array([[9.99726525e-01, 2.73474984e-04]])
and we can see how it predicts on that point.
clf.predict(pt)
array([0])
A single artificial neuron like the function below. where it has parameters that have to be determined before we can use it on an input vector.
def aritificial_neuron_template(activation,weights,bias,inputs):
'''
simple artificial neuron
Parameters
----------
activation : function
activation function of the neuron
weights : numpy aray
wights for summing inputs
bias: numpy array
bias term added to the weighted sum
inputs : numpy array
input to the neuron
'''
return activation(np.matmul(inputs,weights) +bias)
# two common activation functions
identity_activation = lambda x: x
logistic_activation = lambda x: expit(x)
When we instantiate the multilyer perceptron object, MLPClassifier, we pick
the activation function and when we give data to the fit method, we get
the weights and biases.
A neural network passes the data to the hidden layer, and the output of the hidden layer to the output layer. In our neural network, we have just one neuron at each layer.
So the predict_proba method is the same as the following:
aritificial_neuron_template(logistic_activation,clf.coefs_[1],clf.intercepts_[1],
aritificial_neuron_template(identity_activation,clf.coefs_[0],
clf.intercepts_[0],pt))
array([[0.00027347]])
To make this easier to read, we can make the intermediate neurons their own lambda functions.
hidden_neuron = lambda x: aritificial_neuron_template(identity_activation,clf.coefs_[0],clf.intercepts_[0],x)
output_neuron = lambda x: aritificial_neuron_template(expit,clf.coefs_[1],clf.intercepts_[1],x)
output_neuron(hidden_neuron(pt))
array([[0.00027347]])
We can confirm that this works the same as the predict probability method:
clf.predict_proba(pt)
array([[9.99726525e-01, 2.73474984e-04]])
33.3. (optional) What is a numerical optimiztion algorithm?#
Numerical Optimization algorithms are at the core of many of the fit methods.
One way we can optimize a function is to take the derivative, set it equal to zero and sovle for the parameter. If we know the funciton is convex (like a bowl or valley shape) then the place where the derivative (slope) is 0 is the bottom or lowest point of the valley.
Numerial optimzaiton is for when we can’t analytically solve that problem once we set it equal to zero. Optimizaiton algorithms are sort of like search algorithms but can work in high dimensions and use strategy based on calculus.
The basic idea in many numerical optimization algorithms is to start at a point (initial setting of the coefficients in this case) and then compute the value of the function then change the coefficients a little and compute again. We can use those two point to see if the direction we “moved” or the way we changed the parameters made it better or worse. If it was better, we change them more in the same direction, (if we made both smaller then we make them both smaller again) if it got worse, we change in a different direction.
You can think of this like trying to find the bottom of a valley, without being able to see, just check your altitude. You take a step left, right, forward or back and then see if your altitude went up or down.
LBGFS acutally uses the derivative, so it’s like you can see the direction of the hill you’re on, but you have to keep taking steps and then if you reacha point where you can’t go down anymore you know you are done. When the algorithm finds it can’t get better, that’s called convergence.
Stochastic gradient descent works in high dimensions where it’s too hard to do the derivative, but you can randomly move in different directions (or take the partial derivate in a small numbe rof defintions). Adam is a specical version fo that with better strategy.
Numerical optimization is a whole research area. In graduate school, I took a whole semester long course just learning different algorithms for this.