20. Linear Regression

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.model_selection import train_test_split
import pandas as pd
sns.set_theme(font_scale=2,palette='colorblind')

20.1. Setting upa linear regression

tips = sns.load_dataset("tips")

tips.head(1)

	total_bill	tip	sex	smoker	day	time	size
0	16.99	1.01	Female	No	Sun	Dinner	2

We’re going to predict tip from total bill using 80% of the data for training. This is a regression problem because the target, tip is a continuous value, the problems we’ve seen so far were all classification, species of iris and the character in that corners data were both categorical.

Using linear regression is also a good choice because it makes sense that the tip would be approximately linearly related to the total bill, most people pick some percentage of the total bill. If we our prior knowledge was that people typically tipped with some more complicated function, this would not be a good model.

# sklearn requires 2D object of features even for 1 feature
tips_X = tips['total_bill'].values
tips_X = tips_X[:,np.newaxis] # add an axis
tips_y = tips['tip']

tips_X_train,tips_X_test, tips_y_train, tips_y_test = train_test_split(
                                          tips_X,
                                          tips_y,
                                          train_size=.8,
                                          random_state=0)

To see what that new bit of code did, we can examine the shapes:

tips_X.shape

(244, 1)

what we ended up is 2 dimensions (there are two numbers) even though the second one is 1.

tips['total_bill'].values.shape

(244,)

this, without the newaxis is one dimension, we can see that because there is no number after the comma.

Now that our data is ready, we create the linear regression estimator object

regr = linear_model.LinearRegression()

Now we fit the model.

regr.fit(tips_X_train,tips_y_train)

LinearRegression()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

We can examine the coefficients and intercept.

regr.coef_, regr.intercept_

(array([0.0968534]), 1.0285439454607272)

These define a line (y = mx+b) coef is the slope.

Important

This is what our model predicts the tip will be based on the past data. It is important to note that this is not what the tip should be by any sort of virtues. For example, a typical normative rule for tipping is to tip 15% or 20%. the model we learned, from this data, however is ~%10 + \(1. (it's actually 9.68% + \)1.028)

To interpret this, we can apply it for a single value. We trained this to predict the tip from the total bill. So, we can put in any value that’s a plausible total bill and get the predicted tip.

my_bill = np.asarray([17.78]).reshape(1,-1)
regr.predict(my_bill)

array([2.75059744])

We can also apply the function, as usual.

tips_y_pred = regr.predict(tips_X_test)

This gives a vector of values.

tips_y_pred

array([2.7321953 , 2.79999268, 2.91621676, 1.73073111, 2.60434881,
       1.58545101, 2.76415692, 3.28813383, 2.7864332 , 4.38451435,
       3.47699796, 3.47021823, 2.39127132, 2.28763818, 2.32831661,
       3.97288739, 1.83726986, 2.38449158, 2.84745085, 3.26585755,
       3.93995723, 3.05471713, 2.57819839, 2.48521912, 2.33703342,
       2.61693975, 2.20628132, 3.91477534, 3.4779665 , 2.55592211,
       2.45519457, 2.23727441, 2.52202341, 2.05422148, 2.79999268,
       2.32541101, 2.66827205, 2.02903959, 5.7094689 , 2.57626132,
       1.85954614, 2.23243174, 2.54817383, 3.91961801, 2.26439336,
       2.67214619, 2.79515001, 3.11864037, 2.68183153])

To visualize in more detail, we’ll plot the data as black points and the predictions as blue points. To highlight that this is a perfectly linear prediction, we’ll also add a line for the prediction.

plt.scatter(tips_X_test,tips_y_test, color='black')
plt.plot(tips_X_test,tips_y_pred, color='blue')
plt.scatter(tips_X_test,tips_y_pred, color='blue')

<matplotlib.collections.PathCollection at 0x7fe885ac1fa0>

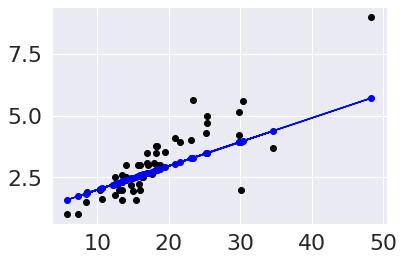
20.2. Evaluating Regression - Mean Squared Error

From the plot, we can see that there is some error for each point, so accuracy that we’ve been using, won’t work. One idea is to look at how much error there is in each prediction, we can look at that visually first.

plt.scatter(tips_X_test, tips_y_test, color='black')
plt.plot(tips_X_test, tips_y_pred, color='blue', linewidth=3)

# draw vertical lines frome each data point to its predict value
[plt.plot([x,x],[yp,yt], color='red', linewidth=3)
         for x, yp, yt in zip(tips_X_test, tips_y_pred,tips_y_test)];

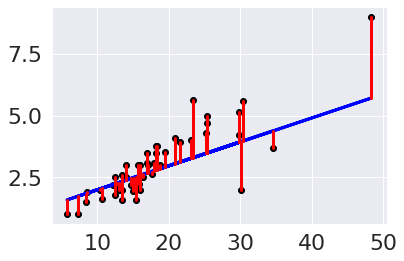
We can use the average length of these red lines to capture the error. To get the length, we can take the difference between the prediction and the data for each point. Some would be positive and others negative, so we will square each one then take the average.

mean_squared_error(tips_y_test, tips_y_pred)

0.821309064276629

We can get back to the units being dollars, by taking the square root.

np.sqrt(mean_squared_error(tips_y_test, tips_y_pred))

0.9062610353957787

This is equivalent to using absolute value instead

np.mean(np.abs(tips_y_test - tips_y_pred))

0.6564074900962107

20.3. Evaluating Regression - R2

We can also use the \(R^2\) regression coefficient.

r2_score(tips_y_test,tips_y_pred)

0.5906895098589039

This is a bit harder to interpret, but we can use some additional plots to visualize. This code simulates data by randomly picking 20 points, spreading them out and makes the “predicted” y values by picking a slope of 3. Then I simulated various levels of noise, by sampling noise and multiplying the same noise vector by different scales and adding all of those to a data frame with the column name the r score for if that column of target values was the truth.

Then I added some columns of y values that were with different slopes and different functions of x. These all have the small amount of noise.

Tip

Facet Grids allow more customization than the figure level plotting functions we have used otherwise, but each of those combines a FacetGrid with a particular type of plot.

x = 10*np.random.random(20)
y_pred = 3*x
ex_df = pd.DataFrame(data = x,columns = ['x'])
ex_df['y_pred'] = y_pred
n_levels = range(1,18,2)
# sample 0 mean noise
noise = (np.random.random(20)-.5)*2
# add varying noise levels
for n in n_levels:
    # add noise, scaled
    y_true = y_pred + n* noise
    # compute the r2 in the column name, assign the "true" (data) here
    ex_df['r2 = '+ str(np.round(r2_score(y_pred,y_true),3))] = y_true

# add functions
f_x_list = [2*x,3.5*x,.5*x**2, .03*x**3, 10*np.sin(x)+x*3,3*np.log(x**2)]
for fx in f_x_list:
    y_true = fx + noise
    # compute the r2 in the column name, assign the "true" (data) here
    ex_df['r2 = '+ str(np.round(r2_score(y_pred,y_true),3))] = y_true  

# melt the data frame for plotting
xy_df = ex_df.melt(id_vars=['x','y_pred'],var_name='rscore',value_name='y')
# create a FacetGrid so that we can add two types of plots per subplot
g = sns.FacetGrid(data = xy_df,col='rscore',col_wrap=3,aspect=1.5,height=3)
g.map(plt.plot, 'x','y_pred',color='k')
g.map(sns.scatterplot, "x", "y",)

<seaborn.axisgrid.FacetGrid at 0x7fe8838ffee0>

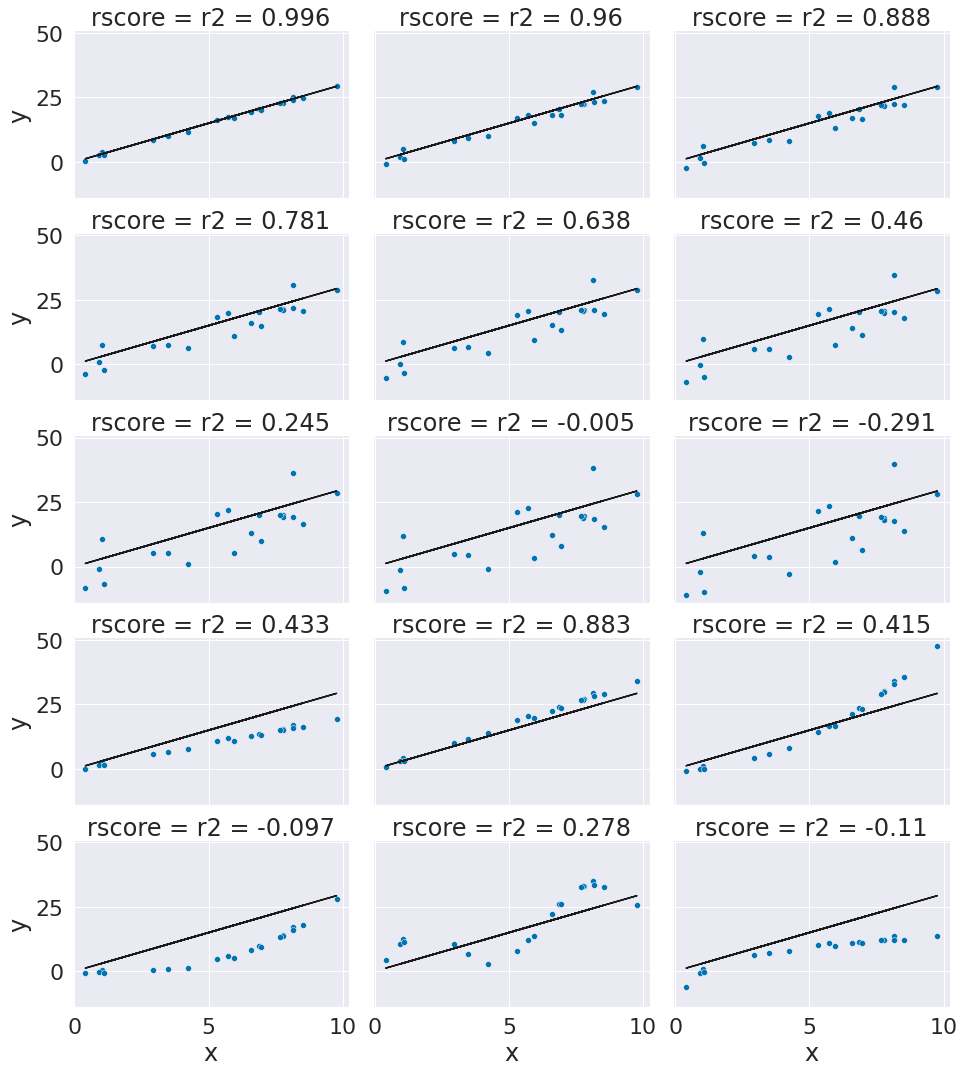
20.4. Multivariate Regression

We can also load data from Scikit learn.

This dataset includes 10 features measured on a given date and an measure of diabetes disease progression measured one year later. The predictor we can train with this data might be someting a doctor uses to calculate a patient’s risk.

diabetes_X, diabetes_y = datasets.load_diabetes(return_X_y = True)

diabetes_X.shape

(442, 10)

diabetes_X_train, diabetes_X_test, diabetes_y_train, diabetes_y_test = train_test_split(
        diabetes_X, diabetes_y)
regr_diabetes = linear_model.LinearRegression()

regr_diabetes.fit(diabetes_X_train,diabetes_y_train)

LinearRegression()

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

20.5. What score does linear regression use?

regr_diabetes.score(diabetes_X_test,diabetes_y_test)

0.43874612898797793

diabetes_y_pred = regr_diabetes.predict(diabetes_X_test)

r2_score(diabetes_y_test,diabetes_y_pred)

0.43874612898797793

mean_squared_error(diabetes_y_test,diabetes_y_pred)

3166.4747190611843

It uses the R2 score.

This model predicts what lab measure a patient will have one year in the future based on lab measures in a given day. Since we see that this is not a very high r2, we can say that this is not a perfect predictor, but a Doctor, who better understands the score would have to help interpret the core.

20.6. Questions After class

20.6.1. How I should use these with data most effectively? What is the proper use of these methods?

To answer continuous prediction tasks, like the ones we saw today. The notes above include more interpretation than we discussed in class, so read carefully for that.

20.6.2. Why is that even when random state is set to 0 numbers are still a little different compared to yours and my neighbor even

random state sets the seed that’s used internally and should work to control the randomness and produce reproducible results. If your results are just a little different, like that it could be a rounding error, maybe you somehow set a default for display that’s different.

See for example these options