Model Comparison
27. Model Comparison#
To compare models, we will first optimize the parameters of two diffrent models and look at how the different parameters settings impact the model comparison. Later, we’ll see how to compare across models of different classes.
import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns
import pandas as pd
from sklearn import datasets
from sklearn import cluster
from sklearn import svm
from sklearn import tree
# import the whole model selection module
from sklearn import model_selection
sns.set_theme(palette='colorblind')
We’ll use the iris data again.
iris_X, iris_y = datasets.load_iris(return_X_y=True)
Remember, we need to split the data into training and test. The cross validation step will hep us optimize the parameters, but we don’t want data leakage where the model has seen the test data multiple times. So, we split the data here for train and test annd the cross validation splits the training data into train and “test” again, but this test is better termed validation.
iris_X_train, iris_X_test, iris_y_train, iris_y_test = model_selection.train_test_split(
iris_X,iris_y, test_size =.2)
Then we can make the object, the parameter grid dictionary and the Grid Search object. We split these into separate cells, so that we can use the built in help to see more detail.
dt = tree.DecisionTreeClassifier()
params_dt = {'criterion':['gini','entropy'],
'max_depth':[2,3,4],
'min_samples_leaf':list(range(2,20,2))}
dt_opt = model_selection.GridSearchCV(dt,params_dt)
Then we fit the Grid search using the training data, and remember this actually resets the parameters and then cross validates multiple times.
dt_opt.fit(iris_X_train,iris_y_train)
GridSearchCV(estimator=DecisionTreeClassifier(),
param_grid={'criterion': ['gini', 'entropy'],
'max_depth': [2, 3, 4],
'min_samples_leaf': [2, 4, 6, 8, 10, 12, 14, 16, 18]})In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook. On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
GridSearchCV(estimator=DecisionTreeClassifier(),
param_grid={'criterion': ['gini', 'entropy'],
'max_depth': [2, 3, 4],
'min_samples_leaf': [2, 4, 6, 8, 10, 12, 14, 16, 18]})DecisionTreeClassifier()
DecisionTreeClassifier()
adn look at the results
dt_opt.cv_results_
{'mean_fit_time': array([0.00039306, 0.00034938, 0.00034437, 0.000349 , 0.00034513,
0.00034647, 0.00034838, 0.00034761, 0.00035162, 0.00038896,
0.00035572, 0.00034981, 0.00035625, 0.00034728, 0.00034947,
0.000349 , 0.00034842, 0.00034723, 0.00035934, 0.00035663,
0.00035768, 0.00035028, 0.00035329, 0.00034971, 0.00035257,
0.00035281, 0.0003489 , 0.00035853, 0.00035596, 0.00035648,
0.0003509 , 0.00035429, 0.00035157, 0.00035481, 0.000353 ,
0.000348 , 0.00036955, 0.00036836, 0.00036283, 0.00036693,
0.00035868, 0.00036645, 0.0003583 , 0.00035987, 0.00035768,
0.0003799 , 0.00037074, 0.00036554, 0.00036526, 0.00036535,
0.00036039, 0.00036349, 0.0003541 , 0.00035987]),
'std_fit_time': array([6.72941413e-05, 8.11268045e-06, 3.81648499e-06, 8.66270211e-06,
4.09525119e-06, 7.54458255e-06, 3.91587547e-06, 3.24809768e-06,
8.48636188e-06, 3.16120380e-05, 9.03854864e-06, 5.72204590e-07,
1.01033231e-05, 1.15430054e-06, 3.76187952e-06, 2.99839209e-06,
3.01050074e-06, 5.62304040e-06, 3.37646503e-06, 2.38609238e-06,
8.43530189e-06, 3.58548569e-06, 9.80059873e-06, 3.46618306e-06,
7.93385961e-06, 8.40289362e-06, 4.56769181e-06, 8.42451299e-06,
1.52289576e-06, 9.17140216e-06, 1.24709099e-06, 9.49133553e-06,
3.84911271e-06, 9.27249058e-06, 1.04203921e-05, 5.76164530e-07,
2.71839005e-06, 7.51680506e-06, 4.13338336e-06, 1.24590533e-05,
2.32430603e-06, 1.30709058e-05, 4.18259854e-06, 8.42208358e-06,
3.00218129e-06, 8.78804544e-06, 8.06545774e-06, 5.73474746e-06,
6.13435761e-06, 6.88794535e-06, 3.65208705e-06, 1.15504882e-05,
3.65768603e-06, 1.35648229e-05]),
'mean_score_time': array([0.00024743, 0.00022221, 0.00022173, 0.00022287, 0.00021906,
0.0002223 , 0.00025768, 0.00025663, 0.00026088, 0.00023623,
0.00022044, 0.00022583, 0.0002223 , 0.00022435, 0.00022206,
0.00022521, 0.0002264 , 0.00022044, 0.00022712, 0.00022411,
0.0002233 , 0.00022063, 0.00022211, 0.00022278, 0.00022445,
0.00022144, 0.00022278, 0.00022326, 0.00022783, 0.00021963,
0.00022578, 0.00021935, 0.00022659, 0.00022411, 0.00022068,
0.00022483, 0.00022292, 0.00022302, 0.00022135, 0.0002223 ,
0.00022497, 0.00022588, 0.00022087, 0.00022306, 0.00022216,
0.00022306, 0.00022664, 0.00022197, 0.00022216, 0.00022125,
0.00022173, 0.00022187, 0.00022726, 0.00022092]),
'std_score_time': array([4.32319092e-05, 3.19160472e-06, 3.24809768e-06, 3.58548569e-06,
8.03580262e-07, 3.42062119e-06, 1.14242063e-06, 2.86102295e-07,
6.98432161e-06, 1.09738869e-05, 9.84180805e-07, 7.53855268e-06,
3.78657946e-06, 8.77561758e-06, 3.19017957e-06, 1.06726340e-05,
1.00810187e-05, 1.04033586e-06, 8.75174819e-06, 5.33759511e-06,
6.38961792e-06, 1.78161065e-06, 2.86340614e-06, 2.90675176e-06,
3.54466773e-06, 1.61280961e-06, 3.74431046e-06, 4.77218475e-06,
7.51014740e-06, 1.01601008e-06, 8.88633093e-06, 5.43678010e-07,
6.88794535e-06, 8.95641852e-06, 8.86968386e-07, 8.29751462e-06,
1.60291064e-06, 1.86271906e-06, 1.24891289e-06, 1.30238536e-06,
9.11569983e-06, 9.07445041e-06, 9.36836372e-07, 2.85545443e-06,
5.09122765e-07, 2.26986508e-06, 7.90112121e-06, 1.28834306e-06,
2.66943646e-06, 1.16800773e-06, 7.83523403e-07, 1.68991519e-06,
8.43260596e-06, 1.16410786e-06]),
'param_criterion': masked_array(data=['gini', 'gini', 'gini', 'gini', 'gini', 'gini', 'gini',
'gini', 'gini', 'gini', 'gini', 'gini', 'gini', 'gini',
'gini', 'gini', 'gini', 'gini', 'gini', 'gini', 'gini',
'gini', 'gini', 'gini', 'gini', 'gini', 'gini',
'entropy', 'entropy', 'entropy', 'entropy', 'entropy',
'entropy', 'entropy', 'entropy', 'entropy', 'entropy',
'entropy', 'entropy', 'entropy', 'entropy', 'entropy',
'entropy', 'entropy', 'entropy', 'entropy', 'entropy',
'entropy', 'entropy', 'entropy', 'entropy', 'entropy',
'entropy', 'entropy'],
mask=[False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False],
fill_value='?',
dtype=object),
'param_max_depth': masked_array(data=[2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3,
4, 4, 4, 4, 4, 4, 4, 4, 4, 2, 2, 2, 2, 2, 2, 2, 2, 2,
3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4],
mask=[False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False],
fill_value='?',
dtype=object),
'param_min_samples_leaf': masked_array(data=[2, 4, 6, 8, 10, 12, 14, 16, 18, 2, 4, 6, 8, 10, 12, 14,
16, 18, 2, 4, 6, 8, 10, 12, 14, 16, 18, 2, 4, 6, 8, 10,
12, 14, 16, 18, 2, 4, 6, 8, 10, 12, 14, 16, 18, 2, 4,
6, 8, 10, 12, 14, 16, 18],
mask=[False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False],
fill_value='?',
dtype=object),
'params': [{'criterion': 'gini', 'max_depth': 2, 'min_samples_leaf': 2},
{'criterion': 'gini', 'max_depth': 2, 'min_samples_leaf': 4},
{'criterion': 'gini', 'max_depth': 2, 'min_samples_leaf': 6},
{'criterion': 'gini', 'max_depth': 2, 'min_samples_leaf': 8},
{'criterion': 'gini', 'max_depth': 2, 'min_samples_leaf': 10},
{'criterion': 'gini', 'max_depth': 2, 'min_samples_leaf': 12},
{'criterion': 'gini', 'max_depth': 2, 'min_samples_leaf': 14},
{'criterion': 'gini', 'max_depth': 2, 'min_samples_leaf': 16},
{'criterion': 'gini', 'max_depth': 2, 'min_samples_leaf': 18},
{'criterion': 'gini', 'max_depth': 3, 'min_samples_leaf': 2},
{'criterion': 'gini', 'max_depth': 3, 'min_samples_leaf': 4},
{'criterion': 'gini', 'max_depth': 3, 'min_samples_leaf': 6},
{'criterion': 'gini', 'max_depth': 3, 'min_samples_leaf': 8},
{'criterion': 'gini', 'max_depth': 3, 'min_samples_leaf': 10},
{'criterion': 'gini', 'max_depth': 3, 'min_samples_leaf': 12},
{'criterion': 'gini', 'max_depth': 3, 'min_samples_leaf': 14},
{'criterion': 'gini', 'max_depth': 3, 'min_samples_leaf': 16},
{'criterion': 'gini', 'max_depth': 3, 'min_samples_leaf': 18},
{'criterion': 'gini', 'max_depth': 4, 'min_samples_leaf': 2},
{'criterion': 'gini', 'max_depth': 4, 'min_samples_leaf': 4},
{'criterion': 'gini', 'max_depth': 4, 'min_samples_leaf': 6},
{'criterion': 'gini', 'max_depth': 4, 'min_samples_leaf': 8},
{'criterion': 'gini', 'max_depth': 4, 'min_samples_leaf': 10},
{'criterion': 'gini', 'max_depth': 4, 'min_samples_leaf': 12},
{'criterion': 'gini', 'max_depth': 4, 'min_samples_leaf': 14},
{'criterion': 'gini', 'max_depth': 4, 'min_samples_leaf': 16},
{'criterion': 'gini', 'max_depth': 4, 'min_samples_leaf': 18},
{'criterion': 'entropy', 'max_depth': 2, 'min_samples_leaf': 2},
{'criterion': 'entropy', 'max_depth': 2, 'min_samples_leaf': 4},
{'criterion': 'entropy', 'max_depth': 2, 'min_samples_leaf': 6},
{'criterion': 'entropy', 'max_depth': 2, 'min_samples_leaf': 8},
{'criterion': 'entropy', 'max_depth': 2, 'min_samples_leaf': 10},
{'criterion': 'entropy', 'max_depth': 2, 'min_samples_leaf': 12},
{'criterion': 'entropy', 'max_depth': 2, 'min_samples_leaf': 14},
{'criterion': 'entropy', 'max_depth': 2, 'min_samples_leaf': 16},
{'criterion': 'entropy', 'max_depth': 2, 'min_samples_leaf': 18},
{'criterion': 'entropy', 'max_depth': 3, 'min_samples_leaf': 2},
{'criterion': 'entropy', 'max_depth': 3, 'min_samples_leaf': 4},
{'criterion': 'entropy', 'max_depth': 3, 'min_samples_leaf': 6},
{'criterion': 'entropy', 'max_depth': 3, 'min_samples_leaf': 8},
{'criterion': 'entropy', 'max_depth': 3, 'min_samples_leaf': 10},
{'criterion': 'entropy', 'max_depth': 3, 'min_samples_leaf': 12},
{'criterion': 'entropy', 'max_depth': 3, 'min_samples_leaf': 14},
{'criterion': 'entropy', 'max_depth': 3, 'min_samples_leaf': 16},
{'criterion': 'entropy', 'max_depth': 3, 'min_samples_leaf': 18},
{'criterion': 'entropy', 'max_depth': 4, 'min_samples_leaf': 2},
{'criterion': 'entropy', 'max_depth': 4, 'min_samples_leaf': 4},
{'criterion': 'entropy', 'max_depth': 4, 'min_samples_leaf': 6},
{'criterion': 'entropy', 'max_depth': 4, 'min_samples_leaf': 8},
{'criterion': 'entropy', 'max_depth': 4, 'min_samples_leaf': 10},
{'criterion': 'entropy', 'max_depth': 4, 'min_samples_leaf': 12},
{'criterion': 'entropy', 'max_depth': 4, 'min_samples_leaf': 14},
{'criterion': 'entropy', 'max_depth': 4, 'min_samples_leaf': 16},
{'criterion': 'entropy', 'max_depth': 4, 'min_samples_leaf': 18}],
'split0_test_score': array([0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333]),
'split1_test_score': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 1., 1.]),
'split2_test_score': array([0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667]),
'split3_test_score': array([0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.95833333,
0.95833333, 0.95833333, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.95833333,
0.95833333, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.95833333, 0.95833333, 0.95833333, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.95833333, 0.95833333, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667]),
'split4_test_score': array([0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 1. , 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333]),
'mean_test_score': array([0.95 , 0.95 , 0.95 , 0.95 , 0.95 ,
0.95 , 0.95 , 0.95 , 0.95 , 0.95833333,
0.95833333, 0.95833333, 0.95 , 0.95 , 0.95 ,
0.95 , 0.95 , 0.95 , 0.95833333, 0.95833333,
0.95833333, 0.95 , 0.95 , 0.95 , 0.95 ,
0.95 , 0.95 , 0.95 , 0.95 , 0.95 ,
0.95 , 0.95 , 0.95 , 0.95 , 0.95 ,
0.95 , 0.95833333, 0.95833333, 0.95833333, 0.95 ,
0.95 , 0.95 , 0.95 , 0.95 , 0.95 ,
0.95 , 0.95833333, 0.95833333, 0.95 , 0.95 ,
0.95 , 0.95 , 0.95 , 0.95 ]),
'std_test_score': array([0.03118048, 0.03118048, 0.03118048, 0.03118048, 0.03118048,
0.03118048, 0.03118048, 0.03118048, 0.03118048, 0.02635231,
0.02635231, 0.02635231, 0.03118048, 0.03118048, 0.03118048,
0.03118048, 0.03118048, 0.03118048, 0.0372678 , 0.02635231,
0.02635231, 0.03118048, 0.03118048, 0.03118048, 0.03118048,
0.03118048, 0.03118048, 0.03118048, 0.03118048, 0.03118048,
0.03118048, 0.03118048, 0.03118048, 0.03118048, 0.03118048,
0.03118048, 0.02635231, 0.02635231, 0.02635231, 0.03118048,
0.03118048, 0.03118048, 0.03118048, 0.03118048, 0.03118048,
0.03118048, 0.02635231, 0.02635231, 0.03118048, 0.03118048,
0.03118048, 0.03118048, 0.03118048, 0.03118048]),
'rank_test_score': array([12, 12, 12, 12, 12, 12, 12, 12, 12, 1, 1, 1, 12, 12, 12, 12, 12,
12, 11, 1, 1, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12,
12, 12, 1, 1, 1, 12, 12, 12, 12, 12, 12, 12, 1, 1, 12, 12, 12,
12, 12, 12], dtype=int32)}
We can reformat it into a dataframe for further analysis.
dt_df = pd.DataFrame(dt_opt.cv_results_)
dt_df.head(2)
| mean_fit_time | std_fit_time | mean_score_time | std_score_time | param_criterion | param_max_depth | param_min_samples_leaf | params | split0_test_score | split1_test_score | split2_test_score | split3_test_score | split4_test_score | mean_test_score | std_test_score | rank_test_score | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.000393 | 0.000067 | 0.000247 | 0.000043 | gini | 2 | 2 | {'criterion': 'gini', 'max_depth': 2, 'min_sam... | 0.958333 | 1.0 | 0.916667 | 0.916667 | 0.958333 | 0.95 | 0.03118 | 12 |
| 1 | 0.000349 | 0.000008 | 0.000222 | 0.000003 | gini | 2 | 4 | {'criterion': 'gini', 'max_depth': 2, 'min_sam... | 0.958333 | 1.0 | 0.916667 | 0.916667 | 0.958333 | 0.95 | 0.03118 | 12 |
Correction
The parameters in this function were in the wrong order in this function in class
I changed the markers and the color of the error bars for readability.
plt.errorbar(x=dt_df['mean_fit_time'],y=dt_df['mean_score_time'],
xerr=dt_df['std_fit_time'],yerr=dt_df['std_score_time'],
marker='s',ecolor='r')
plt.xlabel('fit time')
plt.ylabel('score time')
# save the limits so we can reuse them
xmin, xmax, ymin, ymax = plt.axis()
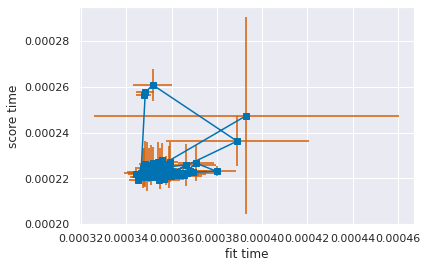
The “points” are at the mean fit and score times. The lines are the “standard deviation” or how much we expect that number to vary, since means are an estimate. Because the data shows an upward trend, this plot tells us that mostly, the models that are slower to fit are also slower to apply. This makes sense for decision trees, deeper trees take longer to learn and longer to traverse when predicting. Because the error bars mostly overlap the other points, this tells us that mostly the variation in time is not a reliable difference. If we re-ran the GridSearch, we could get them in different orders.
To interpret the error bar plot, let’s look at a line plot of just the means, with the same limits so that it’s easier to compare to the plot above.
plt.plot(dt_df['mean_fit_time'],
dt_df['mean_score_time'], marker='s')
plt.xlabel('fit time')
plt.ylabel('score time')
# match the axis limits to above
plt.ylim(ymin, ymax)
plt.xlim(xmin,xmax)
(0.0003190333141088638, 0.00046708042490480804)
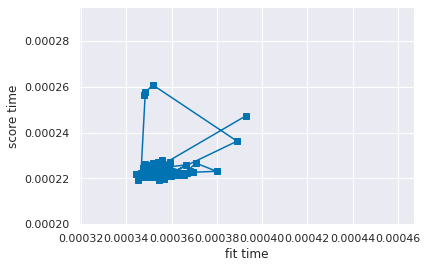
this plot shows the mean times, without the error bars.
dt_df['mean_test_score'].plot(kind='bar')
<AxesSubplot:>
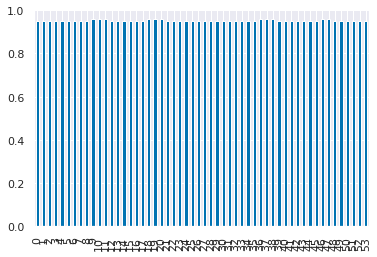
dt_df['mean_test_score']
0 0.950000
1 0.950000
2 0.950000
3 0.950000
4 0.950000
5 0.950000
6 0.950000
7 0.950000
8 0.950000
9 0.958333
10 0.958333
11 0.958333
12 0.950000
13 0.950000
14 0.950000
15 0.950000
16 0.950000
17 0.950000
18 0.958333
19 0.958333
20 0.958333
21 0.950000
22 0.950000
23 0.950000
24 0.950000
25 0.950000
26 0.950000
27 0.950000
28 0.950000
29 0.950000
30 0.950000
31 0.950000
32 0.950000
33 0.950000
34 0.950000
35 0.950000
36 0.958333
37 0.958333
38 0.958333
39 0.950000
40 0.950000
41 0.950000
42 0.950000
43 0.950000
44 0.950000
45 0.950000
46 0.958333
47 0.958333
48 0.950000
49 0.950000
50 0.950000
51 0.950000
52 0.950000
53 0.950000
Name: mean_test_score, dtype: float64
Now let’s compare with a different model, we’ll use the parameter optimized version for that model.
svm_clf = svm.SVC()
param_grid = {'kernel':['linear','rbf'], 'C':[.5, 1, 10]}
svm_opt = GridSearchCV(svm_clf,param_grid,)
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Input In [14], in <cell line: 3>()
1 svm_clf = svm.SVC()
2 param_grid = {'kernel':['linear','rbf'], 'C':[.5, 1, 10]}
----> 3 svm_opt = GridSearchCV(svm_clf,param_grid,)
NameError: name 'GridSearchCV' is not defined
The error above is because we didn’t import GridSearchCV directly today, we imported the whole model_selection module, so we have to use that in order to access the class.
svm_clf = svm.SVC()
param_grid = {'kernel':['linear','rbf'], 'C':[.5, .75,1,2,5,7, 10]}
svm_opt = model_selection.GridSearchCV(svm_clf,param_grid,cv=10)
type(model_selection)
module
dt_opt.__dict__
{'scoring': None,
'estimator': DecisionTreeClassifier(),
'n_jobs': None,
'refit': True,
'cv': None,
'verbose': 0,
'pre_dispatch': '2*n_jobs',
'error_score': nan,
'return_train_score': False,
'param_grid': {'criterion': ['gini', 'entropy'],
'max_depth': [2, 3, 4],
'min_samples_leaf': [2, 4, 6, 8, 10, 12, 14, 16, 18]},
'multimetric_': False,
'best_index_': 9,
'best_score_': 0.9583333333333334,
'best_params_': {'criterion': 'gini', 'max_depth': 3, 'min_samples_leaf': 2},
'best_estimator_': DecisionTreeClassifier(max_depth=3, min_samples_leaf=2),
'refit_time_': 0.00036978721618652344,
'scorer_': <function sklearn.metrics._scorer._passthrough_scorer(estimator, *args, **kwargs)>,
'cv_results_': {'mean_fit_time': array([0.00039306, 0.00034938, 0.00034437, 0.000349 , 0.00034513,
0.00034647, 0.00034838, 0.00034761, 0.00035162, 0.00038896,
0.00035572, 0.00034981, 0.00035625, 0.00034728, 0.00034947,
0.000349 , 0.00034842, 0.00034723, 0.00035934, 0.00035663,
0.00035768, 0.00035028, 0.00035329, 0.00034971, 0.00035257,
0.00035281, 0.0003489 , 0.00035853, 0.00035596, 0.00035648,
0.0003509 , 0.00035429, 0.00035157, 0.00035481, 0.000353 ,
0.000348 , 0.00036955, 0.00036836, 0.00036283, 0.00036693,
0.00035868, 0.00036645, 0.0003583 , 0.00035987, 0.00035768,
0.0003799 , 0.00037074, 0.00036554, 0.00036526, 0.00036535,
0.00036039, 0.00036349, 0.0003541 , 0.00035987]),
'std_fit_time': array([6.72941413e-05, 8.11268045e-06, 3.81648499e-06, 8.66270211e-06,
4.09525119e-06, 7.54458255e-06, 3.91587547e-06, 3.24809768e-06,
8.48636188e-06, 3.16120380e-05, 9.03854864e-06, 5.72204590e-07,
1.01033231e-05, 1.15430054e-06, 3.76187952e-06, 2.99839209e-06,
3.01050074e-06, 5.62304040e-06, 3.37646503e-06, 2.38609238e-06,
8.43530189e-06, 3.58548569e-06, 9.80059873e-06, 3.46618306e-06,
7.93385961e-06, 8.40289362e-06, 4.56769181e-06, 8.42451299e-06,
1.52289576e-06, 9.17140216e-06, 1.24709099e-06, 9.49133553e-06,
3.84911271e-06, 9.27249058e-06, 1.04203921e-05, 5.76164530e-07,
2.71839005e-06, 7.51680506e-06, 4.13338336e-06, 1.24590533e-05,
2.32430603e-06, 1.30709058e-05, 4.18259854e-06, 8.42208358e-06,
3.00218129e-06, 8.78804544e-06, 8.06545774e-06, 5.73474746e-06,
6.13435761e-06, 6.88794535e-06, 3.65208705e-06, 1.15504882e-05,
3.65768603e-06, 1.35648229e-05]),
'mean_score_time': array([0.00024743, 0.00022221, 0.00022173, 0.00022287, 0.00021906,
0.0002223 , 0.00025768, 0.00025663, 0.00026088, 0.00023623,
0.00022044, 0.00022583, 0.0002223 , 0.00022435, 0.00022206,
0.00022521, 0.0002264 , 0.00022044, 0.00022712, 0.00022411,
0.0002233 , 0.00022063, 0.00022211, 0.00022278, 0.00022445,
0.00022144, 0.00022278, 0.00022326, 0.00022783, 0.00021963,
0.00022578, 0.00021935, 0.00022659, 0.00022411, 0.00022068,
0.00022483, 0.00022292, 0.00022302, 0.00022135, 0.0002223 ,
0.00022497, 0.00022588, 0.00022087, 0.00022306, 0.00022216,
0.00022306, 0.00022664, 0.00022197, 0.00022216, 0.00022125,
0.00022173, 0.00022187, 0.00022726, 0.00022092]),
'std_score_time': array([4.32319092e-05, 3.19160472e-06, 3.24809768e-06, 3.58548569e-06,
8.03580262e-07, 3.42062119e-06, 1.14242063e-06, 2.86102295e-07,
6.98432161e-06, 1.09738869e-05, 9.84180805e-07, 7.53855268e-06,
3.78657946e-06, 8.77561758e-06, 3.19017957e-06, 1.06726340e-05,
1.00810187e-05, 1.04033586e-06, 8.75174819e-06, 5.33759511e-06,
6.38961792e-06, 1.78161065e-06, 2.86340614e-06, 2.90675176e-06,
3.54466773e-06, 1.61280961e-06, 3.74431046e-06, 4.77218475e-06,
7.51014740e-06, 1.01601008e-06, 8.88633093e-06, 5.43678010e-07,
6.88794535e-06, 8.95641852e-06, 8.86968386e-07, 8.29751462e-06,
1.60291064e-06, 1.86271906e-06, 1.24891289e-06, 1.30238536e-06,
9.11569983e-06, 9.07445041e-06, 9.36836372e-07, 2.85545443e-06,
5.09122765e-07, 2.26986508e-06, 7.90112121e-06, 1.28834306e-06,
2.66943646e-06, 1.16800773e-06, 7.83523403e-07, 1.68991519e-06,
8.43260596e-06, 1.16410786e-06]),
'param_criterion': masked_array(data=['gini', 'gini', 'gini', 'gini', 'gini', 'gini', 'gini',
'gini', 'gini', 'gini', 'gini', 'gini', 'gini', 'gini',
'gini', 'gini', 'gini', 'gini', 'gini', 'gini', 'gini',
'gini', 'gini', 'gini', 'gini', 'gini', 'gini',
'entropy', 'entropy', 'entropy', 'entropy', 'entropy',
'entropy', 'entropy', 'entropy', 'entropy', 'entropy',
'entropy', 'entropy', 'entropy', 'entropy', 'entropy',
'entropy', 'entropy', 'entropy', 'entropy', 'entropy',
'entropy', 'entropy', 'entropy', 'entropy', 'entropy',
'entropy', 'entropy'],
mask=[False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False],
fill_value='?',
dtype=object),
'param_max_depth': masked_array(data=[2, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 3,
4, 4, 4, 4, 4, 4, 4, 4, 4, 2, 2, 2, 2, 2, 2, 2, 2, 2,
3, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4],
mask=[False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False],
fill_value='?',
dtype=object),
'param_min_samples_leaf': masked_array(data=[2, 4, 6, 8, 10, 12, 14, 16, 18, 2, 4, 6, 8, 10, 12, 14,
16, 18, 2, 4, 6, 8, 10, 12, 14, 16, 18, 2, 4, 6, 8, 10,
12, 14, 16, 18, 2, 4, 6, 8, 10, 12, 14, 16, 18, 2, 4,
6, 8, 10, 12, 14, 16, 18],
mask=[False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False, False, False,
False, False, False, False, False, False],
fill_value='?',
dtype=object),
'params': [{'criterion': 'gini', 'max_depth': 2, 'min_samples_leaf': 2},
{'criterion': 'gini', 'max_depth': 2, 'min_samples_leaf': 4},
{'criterion': 'gini', 'max_depth': 2, 'min_samples_leaf': 6},
{'criterion': 'gini', 'max_depth': 2, 'min_samples_leaf': 8},
{'criterion': 'gini', 'max_depth': 2, 'min_samples_leaf': 10},
{'criterion': 'gini', 'max_depth': 2, 'min_samples_leaf': 12},
{'criterion': 'gini', 'max_depth': 2, 'min_samples_leaf': 14},
{'criterion': 'gini', 'max_depth': 2, 'min_samples_leaf': 16},
{'criterion': 'gini', 'max_depth': 2, 'min_samples_leaf': 18},
{'criterion': 'gini', 'max_depth': 3, 'min_samples_leaf': 2},
{'criterion': 'gini', 'max_depth': 3, 'min_samples_leaf': 4},
{'criterion': 'gini', 'max_depth': 3, 'min_samples_leaf': 6},
{'criterion': 'gini', 'max_depth': 3, 'min_samples_leaf': 8},
{'criterion': 'gini', 'max_depth': 3, 'min_samples_leaf': 10},
{'criterion': 'gini', 'max_depth': 3, 'min_samples_leaf': 12},
{'criterion': 'gini', 'max_depth': 3, 'min_samples_leaf': 14},
{'criterion': 'gini', 'max_depth': 3, 'min_samples_leaf': 16},
{'criterion': 'gini', 'max_depth': 3, 'min_samples_leaf': 18},
{'criterion': 'gini', 'max_depth': 4, 'min_samples_leaf': 2},
{'criterion': 'gini', 'max_depth': 4, 'min_samples_leaf': 4},
{'criterion': 'gini', 'max_depth': 4, 'min_samples_leaf': 6},
{'criterion': 'gini', 'max_depth': 4, 'min_samples_leaf': 8},
{'criterion': 'gini', 'max_depth': 4, 'min_samples_leaf': 10},
{'criterion': 'gini', 'max_depth': 4, 'min_samples_leaf': 12},
{'criterion': 'gini', 'max_depth': 4, 'min_samples_leaf': 14},
{'criterion': 'gini', 'max_depth': 4, 'min_samples_leaf': 16},
{'criterion': 'gini', 'max_depth': 4, 'min_samples_leaf': 18},
{'criterion': 'entropy', 'max_depth': 2, 'min_samples_leaf': 2},
{'criterion': 'entropy', 'max_depth': 2, 'min_samples_leaf': 4},
{'criterion': 'entropy', 'max_depth': 2, 'min_samples_leaf': 6},
{'criterion': 'entropy', 'max_depth': 2, 'min_samples_leaf': 8},
{'criterion': 'entropy', 'max_depth': 2, 'min_samples_leaf': 10},
{'criterion': 'entropy', 'max_depth': 2, 'min_samples_leaf': 12},
{'criterion': 'entropy', 'max_depth': 2, 'min_samples_leaf': 14},
{'criterion': 'entropy', 'max_depth': 2, 'min_samples_leaf': 16},
{'criterion': 'entropy', 'max_depth': 2, 'min_samples_leaf': 18},
{'criterion': 'entropy', 'max_depth': 3, 'min_samples_leaf': 2},
{'criterion': 'entropy', 'max_depth': 3, 'min_samples_leaf': 4},
{'criterion': 'entropy', 'max_depth': 3, 'min_samples_leaf': 6},
{'criterion': 'entropy', 'max_depth': 3, 'min_samples_leaf': 8},
{'criterion': 'entropy', 'max_depth': 3, 'min_samples_leaf': 10},
{'criterion': 'entropy', 'max_depth': 3, 'min_samples_leaf': 12},
{'criterion': 'entropy', 'max_depth': 3, 'min_samples_leaf': 14},
{'criterion': 'entropy', 'max_depth': 3, 'min_samples_leaf': 16},
{'criterion': 'entropy', 'max_depth': 3, 'min_samples_leaf': 18},
{'criterion': 'entropy', 'max_depth': 4, 'min_samples_leaf': 2},
{'criterion': 'entropy', 'max_depth': 4, 'min_samples_leaf': 4},
{'criterion': 'entropy', 'max_depth': 4, 'min_samples_leaf': 6},
{'criterion': 'entropy', 'max_depth': 4, 'min_samples_leaf': 8},
{'criterion': 'entropy', 'max_depth': 4, 'min_samples_leaf': 10},
{'criterion': 'entropy', 'max_depth': 4, 'min_samples_leaf': 12},
{'criterion': 'entropy', 'max_depth': 4, 'min_samples_leaf': 14},
{'criterion': 'entropy', 'max_depth': 4, 'min_samples_leaf': 16},
{'criterion': 'entropy', 'max_depth': 4, 'min_samples_leaf': 18}],
'split0_test_score': array([0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333]),
'split1_test_score': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.,
1., 1., 1.]),
'split2_test_score': array([0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667]),
'split3_test_score': array([0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.95833333,
0.95833333, 0.95833333, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.95833333,
0.95833333, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.95833333, 0.95833333, 0.95833333, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667, 0.91666667,
0.91666667, 0.95833333, 0.95833333, 0.91666667, 0.91666667,
0.91666667, 0.91666667, 0.91666667, 0.91666667]),
'split4_test_score': array([0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 1. , 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333, 0.95833333,
0.95833333, 0.95833333, 0.95833333, 0.95833333]),
'mean_test_score': array([0.95 , 0.95 , 0.95 , 0.95 , 0.95 ,
0.95 , 0.95 , 0.95 , 0.95 , 0.95833333,
0.95833333, 0.95833333, 0.95 , 0.95 , 0.95 ,
0.95 , 0.95 , 0.95 , 0.95833333, 0.95833333,
0.95833333, 0.95 , 0.95 , 0.95 , 0.95 ,
0.95 , 0.95 , 0.95 , 0.95 , 0.95 ,
0.95 , 0.95 , 0.95 , 0.95 , 0.95 ,
0.95 , 0.95833333, 0.95833333, 0.95833333, 0.95 ,
0.95 , 0.95 , 0.95 , 0.95 , 0.95 ,
0.95 , 0.95833333, 0.95833333, 0.95 , 0.95 ,
0.95 , 0.95 , 0.95 , 0.95 ]),
'std_test_score': array([0.03118048, 0.03118048, 0.03118048, 0.03118048, 0.03118048,
0.03118048, 0.03118048, 0.03118048, 0.03118048, 0.02635231,
0.02635231, 0.02635231, 0.03118048, 0.03118048, 0.03118048,
0.03118048, 0.03118048, 0.03118048, 0.0372678 , 0.02635231,
0.02635231, 0.03118048, 0.03118048, 0.03118048, 0.03118048,
0.03118048, 0.03118048, 0.03118048, 0.03118048, 0.03118048,
0.03118048, 0.03118048, 0.03118048, 0.03118048, 0.03118048,
0.03118048, 0.02635231, 0.02635231, 0.02635231, 0.03118048,
0.03118048, 0.03118048, 0.03118048, 0.03118048, 0.03118048,
0.03118048, 0.02635231, 0.02635231, 0.03118048, 0.03118048,
0.03118048, 0.03118048, 0.03118048, 0.03118048]),
'rank_test_score': array([12, 12, 12, 12, 12, 12, 12, 12, 12, 1, 1, 1, 12, 12, 12, 12, 12,
12, 11, 1, 1, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12, 12,
12, 12, 1, 1, 1, 12, 12, 12, 12, 12, 12, 12, 1, 1, 12, 12, 12,
12, 12, 12], dtype=int32)},
'n_splits_': 5}
This doesn’t have attributes yet, even though they are the same type, because we have not fit it tot data yet.
type(svm_opt), type(dt_opt)
(sklearn.model_selection._search.GridSearchCV,
sklearn.model_selection._search.GridSearchCV)
Now we can fit the model to the training data of this second model.
# fit the model and put the CV results in a dataframe
svm_opt.fit(iris_X_train,iris_y_train)
sv_df = pd.DataFrame(svm_opt.cv_results_)
sv_df.head(2)
| mean_fit_time | std_fit_time | mean_score_time | std_score_time | param_C | param_kernel | params | split0_test_score | split1_test_score | split2_test_score | split3_test_score | split4_test_score | split5_test_score | split6_test_score | split7_test_score | split8_test_score | split9_test_score | mean_test_score | std_test_score | rank_test_score | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.000508 | 0.000057 | 0.000272 | 0.000016 | 0.5 | linear | {'C': 0.5, 'kernel': 'linear'} | 1.0 | 1.000000 | 1.000000 | 1.0 | 1.0 | 1.000000 | 0.916667 | 0.916667 | 1.000000 | 1.0 | 0.983333 | 0.033333 | 1 |
| 1 | 0.000606 | 0.000009 | 0.000297 | 0.000008 | 0.5 | rbf | {'C': 0.5, 'kernel': 'rbf'} | 1.0 | 0.916667 | 0.916667 | 1.0 | 1.0 | 0.916667 | 0.916667 | 0.916667 | 0.916667 | 1.0 | 0.950000 | 0.040825 | 14 |
plt.errorbar(x=sv_df['mean_fit_time'],xerr=sv_df['std_fit_time'],
y=sv_df['mean_score_time'],yerr=sv_df['std_score_time'])
<ErrorbarContainer object of 3 artists>
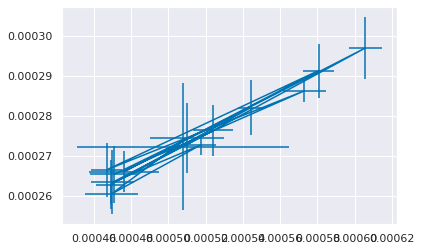
sv_df.columns
Index(['mean_fit_time', 'std_fit_time', 'mean_score_time', 'std_score_time',
'param_C', 'param_kernel', 'params', 'split0_test_score',
'split1_test_score', 'split2_test_score', 'split3_test_score',
'split4_test_score', 'split5_test_score', 'split6_test_score',
'split7_test_score', 'split8_test_score', 'split9_test_score',
'mean_test_score', 'std_test_score', 'rank_test_score'],
dtype='object')
We can see if the models that take longer to fit or score perform better.
svm_time = sv_df.melt(id_vars=['param_C', 'param_kernel', 'params',],
value_vars=['mean_fit_time', 'std_fit_time', 'mean_score_time', 'std_score_time'])
sns.lmplot(data=sv_df, x='mean_fit_time',y='mean_test_score',
hue='param_kernel',fit_reg=False)
<seaborn.axisgrid.FacetGrid at 0x7f261abcdb50>
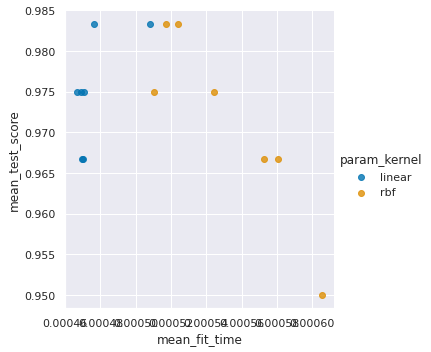
This looks like mostly no.
sns.lmplot(data=sv_df, x='mean_score_time',y='mean_test_score',
hue='param_kernel',fit_reg=False)
<seaborn.axisgrid.FacetGrid at 0x7f261ac35640>
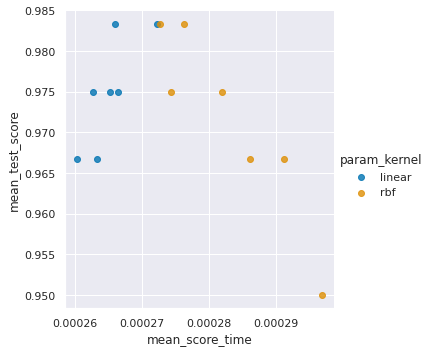
Again, for score time, the slower models don’t appear to be better. Remember though the time differences weren’t that different.
Try it yourself
Try this same analysis for the decision tree, does it matter there?
sv_df_scores = sv_df.melt(id_vars=['param_C', 'param_kernel', 'params',],
value_vars=['split0_test_score',
'split1_test_score', 'split2_test_score', 'split3_test_score',
'split4_test_score'], value_name='score')
sv_df_scores.head()
| param_C | param_kernel | params | variable | score | |
|---|---|---|---|---|---|
| 0 | 0.5 | linear | {'C': 0.5, 'kernel': 'linear'} | split0_test_score | 1.0 |
| 1 | 0.5 | rbf | {'C': 0.5, 'kernel': 'rbf'} | split0_test_score | 1.0 |
| 2 | 0.75 | linear | {'C': 0.75, 'kernel': 'linear'} | split0_test_score | 1.0 |
| 3 | 0.75 | rbf | {'C': 0.75, 'kernel': 'rbf'} | split0_test_score | 1.0 |
| 4 | 1 | linear | {'C': 1, 'kernel': 'linear'} | split0_test_score | 1.0 |
sns.catplot(data=sv_df_scores,x='param_C',y='score',
col='param_kernel')
<seaborn.axisgrid.FacetGrid at 0x7f261ac2e9a0>
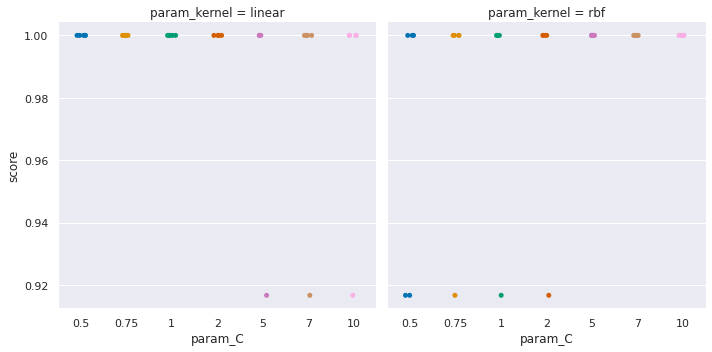
Try it yourself
Try interpretting the plot above, what does it say? what can you conclude from it.
dt_df['mean_test_score'].plot(kind='bar')
<AxesSubplot:>
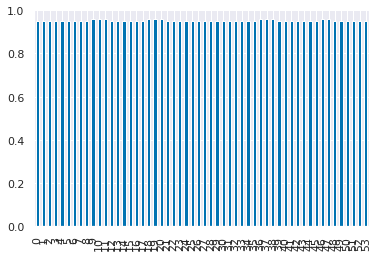
sv_df['mean_test_score'].plot(kind='bar')
<AxesSubplot:>
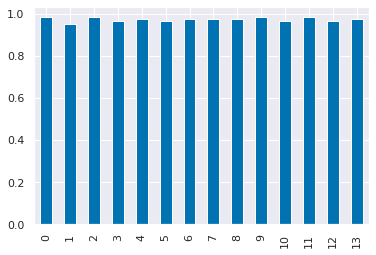
From these last two plots we see that the SVM performance is more sensitive to its parameters, where for the parameters tested, the decision tree is not impacted.
What can we say based on this? We’ll pick up from here on Wednesday.

