Predicting with NN
Contents
39. Predicting with NN#
from scipy.special import expit
from sklearn.datasets import make_classification
from sklearn.neural_network import MLPClassifier
from sklearn import svm
import pandas as pd
import numpy as np
import sklearn
from sklearn import datasets
import matplotlib.pyplot as plt
from sklearn import model_selection
from sklearn.model_selection import train_test_split
import seaborn as sns
sns.set_theme(palette='colorblind')
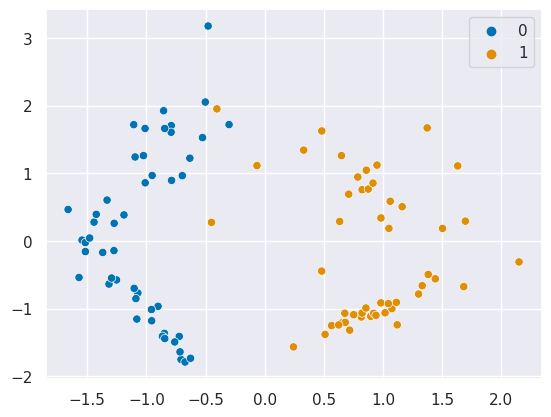
X, y = make_classification(n_samples=100, random_state=1,n_features=2,n_redundant=0)
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, stratify=y,
random_state=1)
sns.scatterplot(x=X[:,0],y=X[:,1],hue=y)
<AxesSubplot: >
clf = MLPClassifier(
hidden_layer_sizes=(1), # 1 hidden layer, 1 aritficial neuron
max_iter=100, # maximum 100 interations in optimization
alpha=1e-4, # regularization
solver="lbfgs", #optimization algorithm
verbose=10, # how much detail to print
activation= 'identity' # how to transform the hidden layer beofore passing it to the next layer
)
clf.fit(X_train, y_train)
clf.score(X_test, y_test)
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 5 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 9.49026D-01 |proj g|= 3.44085D-01
At iterate 1 f= 5.61527D-01 |proj g|= 2.17973D-01
At iterate 2 f= 2.23455D-01 |proj g|= 2.48238D-01
At iterate 3 f= 1.35028D-01 |proj g|= 1.56897D-01
At iterate 4 f= 5.87469D-02 |proj g|= 3.54584D-02
At iterate 5 f= 5.46840D-02 |proj g|= 1.70278D-02
At iterate 6 f= 5.16642D-02 |proj g|= 1.69448D-02
At iterate 7 f= 4.93204D-02 |proj g|= 9.51965D-03
At iterate 8 f= 4.89048D-02 |proj g|= 2.27246D-03
At iterate 9 f= 4.88100D-02 |proj g|= 2.48116D-03
At iterate 10 f= 4.87317D-02 |proj g|= 4.07073D-03
At iterate 11 f= 4.83841D-02 |proj g|= 7.89417D-03
At iterate 12 f= 4.80705D-02 |proj g|= 7.04623D-03
At iterate 13 f= 4.79119D-02 |proj g|= 6.37820D-04
At iterate 14 f= 4.79079D-02 |proj g|= 2.04161D-04
At iterate 15 f= 4.79076D-02 |proj g|= 1.89477D-05
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
5 15 17 1 0 0 1.895D-05 4.791D-02
F = 4.7907579755803981E-002
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
This problem is unconstrained.
1.0
clf.activation
'identity'
clf.out_activation_
'logistic'
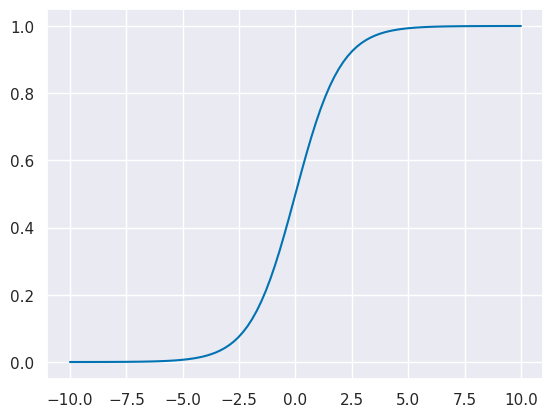
x_logistic = np.linspace(-10,10,100)
y_logistic = expit(x_logistic)
plt.plot(x_logistic,y_logistic)
[<matplotlib.lines.Line2D at 0x7f6bae498d90>]
clf.coefs_
[array([[-5.09240727],
[ 0.14657141]]),
array([[-2.57999695]])]
clf.intercepts_
[array([-1.28067162]), array([2.38983359])]
pt = np.array([[-1,2]])
expit((np.matmul(pt,clf.coefs_[0]) + clf.intercepts_[0])*clf.coefs_[1] + clf.intercepts_[1])
array([[0.00027438]])
clf.predict_proba(pt)
array([[9.99725625e-01, 2.74375013e-04]])
def aritificial_neuron_template(activation,weights,bias,inputs):
'''
simple artificial neuron
Parameters
----------
activation : function
activation function of the neuron
weights : numpy aray
wights for summing inputs one per input
bias: numpy array
bias term added to the weighted sum
inputs : numpy array
input to the neuron, must be same size as weights
'''
return activation(np.matmul(inputs,weights) +bias)
# two common activation functions
identity_activation = lambda x: x
logistic_activation = lambda x: expit(x)
hidden_neuron = lambda x: aritificial_neuron_template(identity_activation,clf.coefs_[0],clf.intercepts_[0],x)
output_neuron = lambda h: aritificial_neuron_template(expit,clf.coefs_[1],clf.intercepts_[1],h)
output_neuron(hidden_neuron(pt))
array([[0.00027438]])
X, y = make_classification(n_samples=200, random_state=1,n_features=4,n_redundant=0,n_informative=4)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y,
random_state=5)
pt_4d =np.asarray([[-1,-2,2,-1],[1.5,0,.5,1]])
clf_4d = MLPClassifier(
hidden_layer_sizes=(1),
max_iter=5000,
alpha=1e-4,
solver="lbfgs",
verbose=10,
activation= 'identity'
)
clf_4d.fit(X_train, y_train)
clf_4d.score(X_test, y_test)
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 7 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 1.09992D+00 |proj g|= 4.72148D-01
At iterate 1 f= 7.07077D-01 |proj g|= 1.62252D-01
At iterate 2 f= 6.56854D-01 |proj g|= 1.29450D-01
At iterate 3 f= 5.35261D-01 |proj g|= 1.39745D-01
At iterate 4 f= 4.55790D-01 |proj g|= 9.59028D-02
At iterate 5 f= 4.42499D-01 |proj g|= 4.61647D-02
At iterate 6 f= 4.35963D-01 |proj g|= 1.22149D-02
At iterate 7 f= 4.34971D-01 |proj g|= 1.02479D-02
At iterate 8 f= 4.34672D-01 |proj g|= 2.89817D-03
At iterate 9 f= 4.34656D-01 |proj g|= 9.79952D-05
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
7 9 10 1 0 0 9.800D-05 4.347D-01
F = 0.43465631975902269
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
This problem is unconstrained.
0.84
df = pd.DataFrame(X,columns=['x0','x1','x2','x3'])
df['y'] = y
sns.pairplot(df,hue='y')
---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
Cell In[15], line 3
1 df = pd.DataFrame(X,columns=['x0','x1','x2','x3'])
2 df['y'] = y
----> 3 sns.pairplot(df,hue='y')
File /opt/hostedtoolcache/Python/3.9.16/x64/lib/python3.9/site-packages/seaborn/axisgrid.py:2148, in pairplot(data, hue, hue_order, palette, vars, x_vars, y_vars, kind, diag_kind, markers, height, aspect, corner, dropna, plot_kws, diag_kws, grid_kws, size)
2146 diag_kws.setdefault("fill", True)
2147 diag_kws.setdefault("warn_singular", False)
-> 2148 grid.map_diag(kdeplot, **diag_kws)
2150 # Maybe plot on the off-diagonals
2151 if diag_kind is not None:
File /opt/hostedtoolcache/Python/3.9.16/x64/lib/python3.9/site-packages/seaborn/axisgrid.py:1507, in PairGrid.map_diag(self, func, **kwargs)
1505 plot_kwargs.setdefault("hue_order", self._hue_order)
1506 plot_kwargs.setdefault("palette", self._orig_palette)
-> 1507 func(x=vector, **plot_kwargs)
1508 ax.legend_ = None
1510 self._add_axis_labels()
File /opt/hostedtoolcache/Python/3.9.16/x64/lib/python3.9/site-packages/seaborn/distributions.py:1717, in kdeplot(data, x, y, hue, weights, palette, hue_order, hue_norm, color, fill, multiple, common_norm, common_grid, cumulative, bw_method, bw_adjust, warn_singular, log_scale, levels, thresh, gridsize, cut, clip, legend, cbar, cbar_ax, cbar_kws, ax, **kwargs)
1713 if p.univariate:
1715 plot_kws = kwargs.copy()
-> 1717 p.plot_univariate_density(
1718 multiple=multiple,
1719 common_norm=common_norm,
1720 common_grid=common_grid,
1721 fill=fill,
1722 color=color,
1723 legend=legend,
1724 warn_singular=warn_singular,
1725 estimate_kws=estimate_kws,
1726 **plot_kws,
1727 )
1729 else:
1731 p.plot_bivariate_density(
1732 common_norm=common_norm,
1733 fill=fill,
(...)
1743 **kwargs,
1744 )
File /opt/hostedtoolcache/Python/3.9.16/x64/lib/python3.9/site-packages/seaborn/distributions.py:996, in _DistributionPlotter.plot_univariate_density(self, multiple, common_norm, common_grid, warn_singular, fill, color, legend, estimate_kws, **plot_kws)
993 if "x" in self.variables:
995 if fill:
--> 996 artist = ax.fill_between(support, fill_from, density, **artist_kws)
998 else:
999 artist, = ax.plot(support, density, **artist_kws)
File /opt/hostedtoolcache/Python/3.9.16/x64/lib/python3.9/site-packages/matplotlib/__init__.py:1423, in _preprocess_data.<locals>.inner(ax, data, *args, **kwargs)
1420 @functools.wraps(func)
1421 def inner(ax, *args, data=None, **kwargs):
1422 if data is None:
-> 1423 return func(ax, *map(sanitize_sequence, args), **kwargs)
1425 bound = new_sig.bind(ax, *args, **kwargs)
1426 auto_label = (bound.arguments.get(label_namer)
1427 or bound.kwargs.get(label_namer))
File /opt/hostedtoolcache/Python/3.9.16/x64/lib/python3.9/site-packages/matplotlib/axes/_axes.py:5367, in Axes.fill_between(self, x, y1, y2, where, interpolate, step, **kwargs)
5365 def fill_between(self, x, y1, y2=0, where=None, interpolate=False,
5366 step=None, **kwargs):
-> 5367 return self._fill_between_x_or_y(
5368 "x", x, y1, y2,
5369 where=where, interpolate=interpolate, step=step, **kwargs)
File /opt/hostedtoolcache/Python/3.9.16/x64/lib/python3.9/site-packages/matplotlib/axes/_axes.py:5272, in Axes._fill_between_x_or_y(self, ind_dir, ind, dep1, dep2, where, interpolate, step, **kwargs)
5268 kwargs["facecolor"] = \
5269 self._get_patches_for_fill.get_next_color()
5271 # Handle united data, such as dates
-> 5272 ind, dep1, dep2 = map(
5273 ma.masked_invalid, self._process_unit_info(
5274 [(ind_dir, ind), (dep_dir, dep1), (dep_dir, dep2)], kwargs))
5276 for name, array in [
5277 (ind_dir, ind), (f"{dep_dir}1", dep1), (f"{dep_dir}2", dep2)]:
5278 if array.ndim > 1:
File /opt/hostedtoolcache/Python/3.9.16/x64/lib/python3.9/site-packages/numpy/ma/core.py:2360, in masked_invalid(a, copy)
2332 def masked_invalid(a, copy=True):
2333 """
2334 Mask an array where invalid values occur (NaNs or infs).
2335
(...)
2357
2358 """
-> 2360 return masked_where(~(np.isfinite(getdata(a))), a, copy=copy)
TypeError: ufunc 'isfinite' not supported for the input types, and the inputs could not be safely coerced to any supported types according to the casting rule ''safe''
hidden_neuron_4d = lambda x: aritificial_neuron_template(identity_activation,
clf_4d.coefs_[0],clf_4d.intercepts_[0],x)
output_neuron_4d = lambda x: aritificial_neuron_template(logistic_activation,
clf_4d.coefs_[1],clf_4d.intercepts_[1],x)
output_neuron_4d(hidden_neuron_4d(pt_4d))
array([[0.95368234],
[0.85341629]])
clf_4d.predict_proba(pt_4d)
array([[0.04631766, 0.95368234],
[0.14658371, 0.85341629]])
clf_4d_4h = MLPClassifier(
hidden_layer_sizes=(4),
max_iter=500,
alpha=1e-4,
solver="lbfgs",
verbose=10,
activation='logistic'
)
clf_4d_4h.fit(X_train, y_train)
clf_4d_4h.score(X_test, y_test)
RUNNING THE L-BFGS-B CODE
* * *
Machine precision = 2.220D-16
N = 25 M = 10
At X0 0 variables are exactly at the bounds
At iterate 0 f= 7.20888D-01 |proj g|= 1.14613D-01
At iterate 1 f= 6.98452D-01 |proj g|= 1.70132D-01
At iterate 2 f= 6.41600D-01 |proj g|= 5.27035D-02
At iterate 3 f= 6.11212D-01 |proj g|= 3.83964D-02
At iterate 4 f= 5.33058D-01 |proj g|= 6.24294D-02
At iterate 5 f= 4.89226D-01 |proj g|= 3.18379D-02
At iterate 6 f= 4.42492D-01 |proj g|= 4.31905D-02
At iterate 7 f= 4.17392D-01 |proj g|= 4.84905D-02
At iterate 8 f= 3.67460D-01 |proj g|= 5.52345D-02
At iterate 9 f= 3.14579D-01 |proj g|= 3.25247D-02
At iterate 10 f= 2.52326D-01 |proj g|= 2.24289D-02
At iterate 11 f= 2.11570D-01 |proj g|= 1.57131D-02
At iterate 12 f= 1.81655D-01 |proj g|= 4.10451D-02
At iterate 13 f= 1.56813D-01 |proj g|= 1.80140D-02
At iterate 14 f= 1.42557D-01 |proj g|= 7.38595D-03
At iterate 15 f= 1.30541D-01 |proj g|= 6.45148D-03
At iterate 16 f= 1.11885D-01 |proj g|= 1.28641D-02
At iterate 17 f= 1.05062D-01 |proj g|= 1.69399D-02
At iterate 18 f= 9.82387D-02 |proj g|= 7.45985D-03
At iterate 19 f= 9.37223D-02 |proj g|= 3.78335D-03
At iterate 20 f= 8.74574D-02 |proj g|= 7.84794D-03
At iterate 21 f= 8.39474D-02 |proj g|= 4.05436D-03
At iterate 22 f= 8.13119D-02 |proj g|= 2.29872D-03
At iterate 23 f= 7.93656D-02 |proj g|= 1.60631D-03
At iterate 24 f= 7.79915D-02 |proj g|= 4.68177D-03
At iterate 25 f= 7.70839D-02 |proj g|= 7.56809D-04
At iterate 26 f= 7.69030D-02 |proj g|= 7.54387D-04
At iterate 27 f= 7.66387D-02 |proj g|= 8.74487D-04
At iterate 28 f= 7.64532D-02 |proj g|= 6.09387D-04
At iterate 29 f= 7.63519D-02 |proj g|= 4.11102D-04
At iterate 30 f= 7.62942D-02 |proj g|= 3.08257D-04
At iterate 31 f= 7.62340D-02 |proj g|= 1.04018D-03
At iterate 32 f= 7.61571D-02 |proj g|= 5.19864D-04
At iterate 33 f= 7.61211D-02 |proj g|= 2.40876D-04
At iterate 34 f= 7.60574D-02 |proj g|= 2.03304D-04
At iterate 35 f= 7.59933D-02 |proj g|= 2.60982D-04
At iterate 36 f= 7.59474D-02 |proj g|= 1.09094D-03
At iterate 37 f= 7.58613D-02 |proj g|= 4.72727D-04
At iterate 38 f= 7.58086D-02 |proj g|= 8.44053D-04
At iterate 39 f= 7.57364D-02 |proj g|= 3.88693D-04
At iterate 40 f= 7.56902D-02 |proj g|= 2.34561D-04
At iterate 41 f= 7.56345D-02 |proj g|= 3.19095D-04
At iterate 42 f= 7.55799D-02 |proj g|= 3.72708D-04
At iterate 43 f= 7.55439D-02 |proj g|= 3.02874D-04
At iterate 44 f= 7.55327D-02 |proj g|= 9.15878D-05
* * *
Tit = total number of iterations
Tnf = total number of function evaluations
Tnint = total number of segments explored during Cauchy searches
Skip = number of BFGS updates skipped
Nact = number of active bounds at final generalized Cauchy point
Projg = norm of the final projected gradient
F = final function value
* * *
N Tit Tnf Tnint Skip Nact Projg F
25 44 48 1 0 0 9.159D-05 7.553D-02
F = 7.5532676171159607E-002
CONVERGENCE: NORM_OF_PROJECTED_GRADIENT_<=_PGTOL
This problem is unconstrained.
0.92
hidden_neuron_4d_h0 = lambda x: aritificial_neuron_template(logistic_activation,
clf_4d_4h.coefs_[0][:,0],clf_4d_4h.intercepts_[0][0],x)
hidden_neuron_4d_h1 = lambda x: aritificial_neuron_template(logistic_activation,
clf_4d_4h.coefs_[0][:,1],clf_4d_4h.intercepts_[0][1],x)
hidden_neuron_4d_h2 = lambda x: aritificial_neuron_template(logistic_activation,
clf_4d_4h.coefs_[0][:,2],clf_4d_4h.intercepts_[0][2],x)
hidden_neuron_4d_h3 = lambda x: aritificial_neuron_template(logistic_activation,
clf_4d_4h.coefs_[0][:,3],clf_4d_4h.intercepts_[0][3],x)
output_neuron_4d_4h = lambda x: aritificial_neuron_template(logistic_activation,
clf_4d_4h.coefs_[1],clf_4d_4h.intercepts_[1],x)
output_neuron_4d_4h(np.asarray([hidden_neuron_4d_h0(pt_4d),
hidden_neuron_4d_h1(pt_4d),
hidden_neuron_4d_h2(pt_4d),
hidden_neuron_4d_h3(pt_4d)]).T)
array([[0.9999897 ],
[0.99999976]])
clf_4d_4h.predict_proba(pt_4d)
array([[1.03043359e-05, 9.99989696e-01],
[2.41212960e-07, 9.99999759e-01]])
39.1. Questions#
39.1.1. Are there neural networks wherein each layer does a different type of transformation, such as logistic or identity?#
There are different types of layers and some are defined by activations, others are more complex calculations in other ways.

